| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 2 Fractions and Decimals
This guide illuminates the solutions for Chapter 2: Fractions and Decimals, significantly advancing the concepts beyond the addition and subtraction covered in Class 6. This chapter focuses squarely on mastering the more intricate operations of multiplication and division for both fractional and decimal representations of numbers. These operations are fundamental for solving a vast array of practical problems, from calculating proportions and areas to understanding financial transactions and scientific measurements. The provided solutions offer comprehensive, step-by-step methods to ensure clarity and proficiency in these essential arithmetic skills.
First, let's delve into the operations with Fractions:
- Multiplication of Fractions: The core rule is explained simply: multiply the numerators together and the denominators together. Symbolically, $\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}$. The solutions also clarify that the word "of" in contexts like "find $\frac{1}{2}$ of 10" signifies multiplication ($\frac{1}{2} \times 10$). Techniques for simplifying fractions (by cancelling common factors between numerators and denominators) either before or after performing the multiplication are demonstrated, leading to results in their simplest form.
- Division of Fractions: This operation hinges on understanding the concept of a reciprocal, or multiplicative inverse. The reciprocal of a non-zero fraction $\frac{c}{d}$ is $\frac{d}{c}$, because $\frac{c}{d} \times \frac{d}{c} = 1$. The solutions clearly articulate the rule for division: dividing by a fraction is equivalent to multiplying by its reciprocal. Thus, $\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}$. The solutions meticulously cover all scenarios:
- Dividing a whole number by a fraction (e.g., $5 \div \frac{1}{2} = 5 \times \frac{2}{1}$).
- Dividing a fraction by a whole number (e.g., $\frac{3}{4} \div 2 = \frac{3}{4} \div \frac{2}{1} = \frac{3}{4} \times \frac{1}{2}$).
- Dividing a fraction by another fraction (using the main rule above).
Next, the solutions address operations with Decimals:
- Multiplication of Decimals: The procedure is broken down: first, multiply the numbers as if they were whole numbers, ignoring the decimal points. Then, count the total number of decimal places in both original factors. Finally, place the decimal point in the product so that it has this total number of decimal places, counting from the right. Special attention is given to multiplication by powers of 10 ($10, 100, 1000, \dots$), which simply involves shifting the decimal point to the right by the number of zeros in the power of 10.
- Division of Decimals: This is explained systematically:
- Division by whole numbers: Perform standard long division, placing the decimal point in the quotient directly above its position in the dividend.
- Division by powers of 10 ($10, 100, 1000, \dots$): This involves shifting the decimal point in the dividend to the left by the number of zeros in the power of 10.
- Division by another decimal: This critical technique involves converting the divisor into a whole number by multiplying both the divisor and the dividend by the same appropriate power of 10 (e.g., 10, 100). For example, to compute $15.5 \div 0.5$, multiply both by 10 to get the equivalent problem $155 \div 5$, which is then easily solved.
Across both fractions and decimals, the solutions provide numerous worked examples for all multiplication and division scenarios, ensuring procedural fluency. A significant emphasis is placed on word problems, demonstrating the practical relevance of these operations. Solutions guide students in translating real-life situations—calculating the area of a rectangular plot with dimensions like $5.5$ m by $3.2$ m, finding the distance covered if speed is $12\frac{1}{2}$ km/h and time is $2\frac{1}{4}$ hours, determining the cost of items (e.g., finding the cost of $3.5$ kg of apples if 1 kg costs $\textsf{₹}80.50$), dividing quantities into portions, or converting units (like km to m, kg to g)—into the correct mathematical operations ($\times$ or $\div$). The careful breakdown, accurate calculation, and presentation of answers with appropriate units are key features of these solutions.
Example 1 to 4 (Before Exercise 2.1)
Example 1 Write five equivalent fractions of $\frac{3}{5}$ .
Answer:
Solution:
To find equivalent fractions of a given fraction, we multiply both the numerator and the denominator by the same non-zero integer.
The given fraction is $\frac{3}{5}$.
We can find five equivalent fractions by multiplying the numerator and denominator by integers like 2, 3, 4, 5, 6, etc.
1. Multiply by 2:
$\frac{3}{5} = \frac{3 \times 2}{5 \times 2} = \frac{6}{10}$
2. Multiply by 3:
$\frac{3}{5} = \frac{3 \times 3}{5 \times 3} = \frac{9}{15}$
3. Multiply by 4:
$\frac{3}{5} = \frac{3 \times 4}{5 \times 4} = \frac{12}{20}$
4. Multiply by 5:
$\frac{3}{5} = \frac{3 \times 5}{5 \times 5} = \frac{15}{25}$
5. Multiply by 6:
$\frac{3}{5} = \frac{3 \times 6}{5 \times 6} = \frac{18}{30}$
Thus, five equivalent fractions of $\frac{3}{5}$ are $\mathbf{\frac{6}{10}, \frac{9}{15}, \frac{12}{20}, \frac{15}{25}, \frac{18}{30}}$.
Example 2 Ramesh solved $\frac{2}{7}$ part of an exercise while Seema solved $\frac{4}{5}$ of it. Who solved lesser part?
Answer:
Solution:
Ramesh solved $\frac{2}{7}$ part of the exercise.
Seema solved $\frac{4}{5}$ part of the exercise.
To find who solved a lesser part, we need to compare the two fractions $\frac{2}{7}$ and $\frac{4}{5}$.
To compare fractions with different denominators, we find a common denominator.
The denominators are 7 and 5.
The Least Common Multiple (LCM) of 7 and 5 is $7 \times 5 = 35$, as 7 and 5 are prime numbers.
Now, we convert both fractions to equivalent fractions with a denominator of 35.
For Ramesh's part: $\frac{2}{7}$
To get a denominator of 35, we multiply the denominator 7 by 5. We must also multiply the numerator by 5.
$\frac{2}{7} = \frac{2 \times 5}{7 \times 5} = \frac{10}{35}$
So, Ramesh solved $\frac{10}{35}$ part of the exercise.
For Seema's part: $\frac{4}{5}$
To get a denominator of 35, we multiply the denominator 5 by 7. We must also multiply the numerator by 7.
$\frac{4}{5} = \frac{4 \times 7}{5 \times 7} = \frac{28}{35}$
So, Seema solved $\frac{28}{35}$ part of the exercise.
Now we compare the two fractions with the same denominator: $\frac{10}{35}$ and $\frac{28}{35}$.
When comparing fractions with the same denominator, the fraction with the smaller numerator is the smaller fraction.
Comparing the numerators, we have 10 and 28.
Since $10 < 28$, we have $\frac{10}{35} < \frac{28}{35}$.
This means $\frac{2}{7} < \frac{4}{5}$.
Since Ramesh solved $\frac{2}{7}$ part and Seema solved $\frac{4}{5}$ part, and $\frac{2}{7}$ is less than $\frac{4}{5}$, Ramesh solved the lesser part.
Therefore, Ramesh solved the lesser part.
Example 3 Sameera purchased $3\frac{1}{2}$ kg apples and $4\frac{3}{4}$ kg oranges. What is the total weight of fruits purchased by her?
Answer:
Given:
Weight of apples purchased by Sameera = $3\frac{1}{2}$ kg.
Weight of oranges purchased by Sameera = $4\frac{3}{4}$ kg.
To Find:
The total weight of fruits purchased by Sameera.
Solution:
The total weight of fruits is the sum of the weight of apples and the weight of oranges.
Total weight = Weight of apples + Weight of oranges
Total weight = $3\frac{1}{2} + 4\frac{3}{4}$ kg.
First, convert the mixed numbers to improper fractions.
$3\frac{1}{2} = \frac{(3 \times 2) + 1}{2} = \frac{6 + 1}{2} = \frac{7}{2}$
$4\frac{3}{4} = \frac{(4 \times 4) + 3}{4} = \frac{16 + 3}{4} = \frac{19}{4}$
Now, we need to add $\frac{7}{2}$ and $\frac{19}{4}$.
The denominators are 2 and 4. The Least Common Multiple (LCM) of 2 and 4 is 4.
Convert $\frac{7}{2}$ to an equivalent fraction with a denominator of 4:
$\frac{7}{2} = \frac{7 \times 2}{2 \times 2} = \frac{14}{4}$
Now, add the fractions:
Total weight = $\frac{14}{4} + \frac{19}{4}$
Total weight = $\frac{14 + 19}{4} = \frac{33}{4}$ kg.
The total weight is $\frac{33}{4}$ kg.
We can convert this improper fraction back to a mixed number.
Divide 33 by 4:
$33 \div 4 = 8$ with a remainder of $1$.
So, $\frac{33}{4} = 8\frac{1}{4}$.
Thus, the total weight of fruits purchased by Sameera is $\mathbf{8\frac{1}{4}}$ kg.
Example 4 Suman studies for $5\frac{2}{3}$ hours daily. She devotes $2\frac{4}{5}$ hours of her time for Science and Mathematics. How much time does she devote for other subjects?
Answer:
Given:
Total time Suman studies daily = $5\frac{2}{3}$ hours.
Time devoted for Science and Mathematics = $2\frac{4}{5}$ hours.
To Find:
Time devoted for other subjects.
Solution:
The time devoted for other subjects is the total study time minus the time devoted for Science and Mathematics.
Time for other subjects = Total study time - Time for Science and Mathematics
Time for other subjects = $5\frac{2}{3} - 2\frac{4}{5}$ hours.
First, convert the mixed numbers to improper fractions:
$5\frac{2}{3} = \frac{(5 \times 3) + 2}{3} = \frac{15 + 2}{3} = \frac{17}{3}$
$2\frac{4}{5} = \frac{(2 \times 5) + 4}{5} = \frac{10 + 4}{5} = \frac{14}{5}$
Now, we need to subtract $\frac{14}{5}$ from $\frac{17}{3}$.
We need a common denominator to subtract the fractions. The denominators are 3 and 5. The Least Common Multiple (LCM) of 3 and 5 is 15.
Convert both fractions to equivalent fractions with a denominator of 15:
$\frac{17}{3} = \frac{17 \times 5}{3 \times 5} = \frac{85}{15}$
$\frac{14}{5} = \frac{14 \times 3}{5 \times 3} = \frac{42}{15}$
Now, perform the subtraction:
Time for other subjects = $\frac{85}{15} - \frac{42}{15}$
Time for other subjects = $\frac{85 - 42}{15} = \frac{43}{15}$ hours.
The time devoted for other subjects is $\frac{43}{15}$ hours.
We can convert this improper fraction back to a mixed number.
Divide 43 by 15:
$43 \div 15 = 2$ with a remainder of $13$.
So, $\frac{43}{15} = 2\frac{13}{15}$.
Thus, Suman devotes $\mathbf{2\frac{13}{15}}$ hours for other subjects.
Exercise 2.1
Question 1. Solve:
(i) $2 - \frac{3}{5}$
(ii) $4 + \frac{7}{8}$
(iii) $\frac{3}{5} + \frac{2}{7}$
(iv) $\frac{9}{11} - \frac{4}{15}$
(v) $\frac{7}{10} + \frac{2}{5} + \frac{3}{2}$
(vi) $2\frac{2}{3} + 3\frac{1}{2}$
(vii) $8\frac{1}{2} - 3\frac{5}{8}$
Answer:
Solution:
(i) $2 - \frac{3}{5}$
We can write $2$ as $\frac{2}{1}$.
So, we have $\frac{2}{1} - \frac{3}{5}$.
The denominators are 1 and 5. The LCM of 1 and 5 is 5.
Convert $\frac{2}{1}$ to an equivalent fraction with denominator 5:
$\frac{2}{1} = \frac{2 \times 5}{1 \times 5} = \frac{10}{5}$
Now subtract:
$\frac{10}{5} - \frac{3}{5} = \frac{10 - 3}{5} = \frac{7}{5}$
The answer is $\mathbf{\frac{7}{5}}$. This can also be written as a mixed number $1\frac{2}{5}$.
(ii) $4 + \frac{7}{8}$
We can write $4$ as $\frac{4}{1}$.
So, we have $\frac{4}{1} + \frac{7}{8}$.
The denominators are 1 and 8. The LCM of 1 and 8 is 8.
Convert $\frac{4}{1}$ to an equivalent fraction with denominator 8:
$\frac{4}{1} = \frac{4 \times 8}{1 \times 8} = \frac{32}{8}$
Now add:
$\frac{32}{8} + \frac{7}{8} = \frac{32 + 7}{8} = \frac{39}{8}$
The answer is $\mathbf{\frac{39}{8}}$. This can also be written as a mixed number $4\frac{7}{8}$.
(iii) $\frac{3}{5} + \frac{2}{7}$
The denominators are 5 and 7. The LCM of 5 and 7 is $5 \times 7 = 35$.
Convert both fractions to equivalent fractions with denominator 35:
$\frac{3}{5} = \frac{3 \times 7}{5 \times 7} = \frac{21}{35}$
$\frac{2}{7} = \frac{2 \times 5}{7 \times 5} = \frac{10}{35}$
Now add:
$\frac{21}{35} + \frac{10}{35} = \frac{21 + 10}{35} = \frac{31}{35}$
The answer is $\mathbf{\frac{31}{35}}$.
(iv) $\frac{9}{11} - \frac{4}{15}$
The denominators are 11 and 15. The LCM of 11 and 15 is $11 \times 15 = 165$.
Convert both fractions to equivalent fractions with denominator 165:
$\frac{9}{11} = \frac{9 \times 15}{11 \times 15} = \frac{135}{165}$
$\frac{4}{15} = \frac{4 \times 11}{15 \times 11} = \frac{44}{165}$
Now subtract:
$\frac{135}{165} - \frac{44}{165} = \frac{135 - 44}{165} = \frac{91}{165}$
The answer is $\mathbf{\frac{91}{165}}$.
(v) $\frac{7}{10} + \frac{2}{5} + \frac{3}{2}$
The denominators are 10, 5, and 2. The LCM of 10, 5, and 2 is 10.
Convert all fractions to equivalent fractions with denominator 10:
$\frac{7}{10}$ already has denominator 10.
$\frac{2}{5} = \frac{2 \times 2}{5 \times 2} = \frac{4}{10}$
$\frac{3}{2} = \frac{3 \times 5}{2 \times 5} = \frac{15}{10}$
Now add:
$\frac{7}{10} + \frac{4}{10} + \frac{15}{10} = \frac{7 + 4 + 15}{10} = \frac{26}{10}$
The fraction $\frac{26}{10}$ can be simplified by dividing both numerator and denominator by their greatest common divisor, which is 2.
$\frac{26 \div 2}{10 \div 2} = \frac{13}{5}$
The answer is $\mathbf{\frac{13}{5}}$. This can also be written as a mixed number $2\frac{3}{5}$.
(vi) $2\frac{2}{3} + 3\frac{1}{2}$
Convert the mixed numbers to improper fractions:
$2\frac{2}{3} = \frac{(2 \times 3) + 2}{3} = \frac{6 + 2}{3} = \frac{8}{3}$
$3\frac{1}{2} = \frac{(3 \times 2) + 1}{2} = \frac{6 + 1}{2} = \frac{7}{2}$
Now we need to add $\frac{8}{3}$ and $\frac{7}{2}$.
The denominators are 3 and 2. The LCM of 3 and 2 is 6.
Convert both fractions to equivalent fractions with denominator 6:
$\frac{8}{3} = \frac{8 \times 2}{3 \times 2} = \frac{16}{6}$
$\frac{7}{2} = \frac{7 \times 3}{2 \times 3} = \frac{21}{6}$
Now add:
$\frac{16}{6} + \frac{21}{6} = \frac{16 + 21}{6} = \frac{37}{6}$
The answer is $\mathbf{\frac{37}{6}}$. This can also be written as a mixed number $6\frac{1}{6}$.
(vii) $8\frac{1}{2} - 3\frac{5}{8}$
Convert the mixed numbers to improper fractions:
$8\frac{1}{2} = \frac{(8 \times 2) + 1}{2} = \frac{16 + 1}{2} = \frac{17}{2}$
$3\frac{5}{8} = \frac{(3 \times 8) + 5}{8} = \frac{24 + 5}{8} = \frac{29}{8}$
Now we need to subtract $\frac{29}{8}$ from $\frac{17}{2}$.
The denominators are 2 and 8. The LCM of 2 and 8 is 8.
Convert $\frac{17}{2}$ to an equivalent fraction with denominator 8:
$\frac{17}{2} = \frac{17 \times 4}{2 \times 4} = \frac{68}{8}$
Now subtract:
$\frac{68}{8} - \frac{29}{8} = \frac{68 - 29}{8} = \frac{39}{8}$
The answer is $\mathbf{\frac{39}{8}}$. This can also be written as a mixed number $4\frac{7}{8}$.
Question 2. Arrange the following in descending order:
(i) $\frac{2}{9}$ , $\frac{2}{3}$ , $\frac{8}{21}$
(ii) $\frac{1}{5}$ , $\frac{3}{7}$ , $\frac{7}{10}$
Answer:
Solution:
(i) $\frac{2}{9}$, $\frac{2}{3}$, $\frac{8}{21}$
To arrange the fractions in descending order, we first find a common denominator for all fractions.
The denominators are 9, 3, and 21.
We find the Least Common Multiple (LCM) of 9, 3, and 21.
Prime factorization of the denominators:
$9 = 3 \times 3 = 3^2$
$3 = 3^1$
$21 = 3 \times 7$
LCM(9, 3, 21) = $3^2 \times 7 = 9 \times 7 = 63$.
Now, convert each fraction to an equivalent fraction with denominator 63.
For $\frac{2}{9}$:
$\frac{2}{9} = \frac{2 \times 7}{9 \times 7} = \frac{14}{63}$
For $\frac{2}{3}$:
$\frac{2}{3} = \frac{2 \times 21}{3 \times 21} = \frac{42}{63}$
For $\frac{8}{21}$:
$\frac{8}{21} = \frac{8 \times 3}{21 \times 3} = \frac{24}{63}$
Now compare the equivalent fractions: $\frac{14}{63}$, $\frac{42}{63}$, $\frac{24}{63}$.
Since the denominators are the same, we compare the numerators: 14, 42, and 24.
Arranging the numerators in descending order: $42 > 24 > 14$.
So, the fractions in descending order are $\frac{42}{63} > \frac{24}{63} > \frac{14}{63}$.
Substituting back the original fractions:
$\frac{2}{3} > \frac{8}{21} > \frac{2}{9}$.
The fractions in descending order are $\mathbf{\frac{2}{3}, \frac{8}{21}, \frac{2}{9}}$.
(ii) $\frac{1}{5}$, $\frac{3}{7}$, $\frac{7}{10}$
To arrange the fractions in descending order, we first find a common denominator for all fractions.
The denominators are 5, 7, and 10.
We find the Least Common Multiple (LCM) of 5, 7, and 10.
Prime factorization of the denominators:
$5 = 5^1$
$7 = 7^1$
$10 = 2 \times 5$
LCM(5, 7, 10) = $2 \times 5 \times 7 = 70$.
Now, convert each fraction to an equivalent fraction with denominator 70.
For $\frac{1}{5}$:
$\frac{1}{5} = \frac{1 \times 14}{5 \times 14} = \frac{14}{70}$
For $\frac{3}{7}$:
$\frac{3}{7} = \frac{3 \times 10}{7 \times 10} = \frac{30}{70}$
For $\frac{7}{10}$:
$\frac{7}{10} = \frac{7 \times 7}{10 \times 7} = \frac{49}{70}$
Now compare the equivalent fractions: $\frac{14}{70}$, $\frac{30}{70}$, $\frac{49}{70}$.
Since the denominators are the same, we compare the numerators: 14, 30, and 49.
Arranging the numerators in descending order: $49 > 30 > 14$.
So, the fractions in descending order are $\frac{49}{70} > \frac{30}{70} > \frac{14}{70}$.
Substituting back the original fractions:
$\frac{7}{10} > \frac{3}{7} > \frac{1}{5}$.
The fractions in descending order are $\mathbf{\frac{7}{10}, \frac{3}{7}, \frac{1}{5}}$.
Question 3. In a “magic square”, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?
| $\frac{4}{11}$ | $\frac{9}{11}$ | $\frac{2}{11}$ |
| $\frac{3}{11}$ | $\frac{5}{11}$ | $\frac{7}{11}$ |
| $\frac{8}{11}$ | $\frac{1}{11}$ | $\frac{6}{11}$ |
(Along the first row $\frac{4}{11} + \frac{9}{11} + \frac{2}{11} = \frac{15}{11}$).
Answer:
Solution:
To check if the given square is a magic square, we need to calculate the sum of the numbers in each row, each column, and along both diagonals. If all these sums are equal, then it is a magic square.
Sum of Rows:
Sum of Row 1 = $\frac{4}{11} + \frac{9}{11} + \frac{2}{11} = \frac{4+9+2}{11} = \frac{15}{11}$
Sum of Row 2 = $\frac{3}{11} + \frac{5}{11} + \frac{7}{11} = \frac{3+5+7}{11} = \frac{15}{11}$
Sum of Row 3 = $\frac{8}{11} + \frac{1}{11} + \frac{6}{11} = \frac{8+1+6}{11} = \frac{15}{11}$
All row sums are equal to $\frac{15}{11}$.
Sum of Columns:
Sum of Column 1 = $\frac{4}{11} + \frac{3}{11} + \frac{8}{11} = \frac{4+3+8}{11} = \frac{15}{11}$
Sum of Column 2 = $\frac{9}{11} + \frac{5}{11} + \frac{1}{11} = \frac{9+5+1}{11} = \frac{15}{11}$
Sum of Column 3 = $\frac{2}{11} + \frac{7}{11} + \frac{6}{11} = \frac{2+7+6}{11} = \frac{15}{11}$
All column sums are equal to $\frac{15}{11}$.
Sum of Diagonals:
Sum of Diagonal 1 (top-left to bottom-right) = $\frac{4}{11} + \frac{5}{11} + \frac{6}{11} \ $$ = \frac{4+5+6}{11} \ $$ = \frac{15}{11}$
Sum of Diagonal 2 (top-right to bottom-left) = $\frac{2}{11} + \frac{5}{11} + \frac{8}{11} \ $$ = \frac{2+5+8}{11} \ $$ = \frac{15}{11}$
All diagonal sums are equal to $\frac{15}{11}$.
Since the sum of the numbers in each row, in each column, and along both diagonals is the same ($\frac{15}{11}$), the given square is a magic square.
Therefore, the answer is Yes, this is a magic square.
Question 4. A rectangular sheet of paper is $12\frac{1}{2}$ cm long and $10\frac{2}{3}$ cm wide. Find its perimeter.
Answer:
Given:
Length of the rectangular sheet, $l = 12\frac{1}{2}$ cm.
Width of the rectangular sheet, $w = 10\frac{2}{3}$ cm.
To Find:
The perimeter of the rectangular sheet.
Solution:
First, convert the given mixed numbers into improper fractions.
Length $l = 12\frac{1}{2} = \frac{(12 \times 2) + 1}{2} = \frac{24 + 1}{2} = \frac{25}{2}$ cm.
Width $w = 10\frac{2}{3} = \frac{(10 \times 3) + 2}{3} = \frac{30 + 2}{3} = \frac{32}{3}$ cm.
The formula for the perimeter of a rectangle is $P = 2 \times (l + w)$.
Substitute the values of $l$ and $w$ into the formula:
$P = 2 \times \left(\frac{25}{2} + \frac{32}{3}\right)$
First, add the fractions inside the brackets. We need a common denominator for 2 and 3, which is the LCM of 2 and 3. LCM(2, 3) = 6.
Convert the fractions to have a denominator of 6:
$\frac{25}{2} = \frac{25 \times 3}{2 \times 3} = \frac{75}{6}$
$\frac{32}{3} = \frac{32 \times 2}{3 \times 2} = \frac{64}{6}$
Now add the converted fractions:
$\frac{25}{2} + \frac{32}{3} = \frac{75}{6} + \frac{64}{6} = \frac{75 + 64}{6} = \frac{139}{6}$
Now, multiply the sum by 2 to find the perimeter:
$P = 2 \times \frac{139}{6}$
$P = \frac{2}{1} \times \frac{139}{6}$
We can cancel out the common factor of 2 from the numerator and the denominator:
$P = \frac{\cancel{2}^{1} \times 139}{1 \times \cancel{6}_{3}} = \frac{1 \times 139}{1 \times 3} = \frac{139}{3}$
The perimeter is $\frac{139}{3}$ cm.
We can also express this as a mixed number by dividing 139 by 3:
$139 \div 3 = 46$ with a remainder of $1$.
So, $\frac{139}{3} = 46\frac{1}{3}$ cm.
The perimeter of the rectangular sheet is $\mathbf{46\frac{1}{3}}$ cm or $\mathbf{\frac{139}{3}}$ cm.
Question 5.
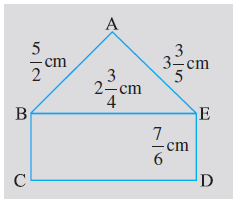
Find the perimeters of
(i) ∆ABE
(ii) the rectangle BCDE in this figure.
Whose perimeter is greater?
Answer:
To Find:
(i) The perimeter of ∆ABE.
(ii) The perimeter of the rectangle BCDE.
And to determine whose perimeter is greater.
(i) Perimeter of ∆ABE
The perimeter of a triangle is the sum of the lengths of its three sides.
From the figure, the side lengths of ∆ABE are:
Side AB = $\frac{5}{2}$ cm
Side BE = $2\frac{3}{4}$ cm
Side AE = $3\frac{3}{5}$ cm
Perimeter of ∆ABE = $AB + BE + AE$
$= \frac{5}{2} + 2\frac{3}{4} + 3\frac{3}{5}$
First, we convert the mixed fractions into improper fractions:
$2\frac{3}{4} = \frac{(2 \times 4) + 3}{4} = \frac{8+3}{4} = \frac{11}{4}$
$3\frac{3}{5} = \frac{(3 \times 5) + 3}{5} = \frac{15+3}{5} = \frac{18}{5}$
Now, we add the fractions:
Perimeter = $\frac{5}{2} + \frac{11}{4} + \frac{18}{5}$
To add these fractions, we need to find a common denominator, which is the LCM of 2, 4, and 5. The LCM of 2, 4, and 5 is 20.
$= \frac{5 \times 10}{2 \times 10} + \frac{11 \times 5}{4 \times 5} + \frac{18 \times 4}{5 \times 4}$
$= \frac{50}{20} + \frac{55}{20} + \frac{72}{20}$
$= \frac{50 + 55 + 72}{20} = \frac{177}{20}$
Converting back to a mixed fraction: $177 \div 20 = 8$ with a remainder of 17.
Perimeter of ∆ABE = $8\frac{17}{20}$ cm.
(ii) Perimeter of the rectangle BCDE
The perimeter of a rectangle is given by the formula: 2 × (length + width).
From the figure, the dimensions of the rectangle BCDE are:
Length (BE) = $2\frac{3}{4}$ cm
Width (ED) = $\frac{7}{6}$ cm
Perimeter of rectangle BCDE = $2 \times (BE + ED)$
$= 2 \times (2\frac{3}{4} + \frac{7}{6})$
First, convert the mixed fraction to an improper fraction: $2\frac{3}{4} = \frac{11}{4}$.
$= 2 \times (\frac{11}{4} + \frac{7}{6})$
Now, add the fractions inside the parentheses. The LCM of 4 and 6 is 12.
$= 2 \times (\frac{11 \times 3}{4 \times 3} + \frac{7 \times 2}{6 \times 2})$
$= 2 \times (\frac{33}{12} + \frac{14}{12})$
$= 2 \times (\frac{33 + 14}{12})$
$= 2 \times \frac{47}{12} = \frac{\cancel{2}^{1} \times 47}{\cancel{12}_{6}} = \frac{47}{6}$
Converting back to a mixed fraction: $47 \div 6 = 7$ with a remainder of 5.
Perimeter of rectangle BCDE = $7\frac{5}{6}$ cm.
Comparison of Perimeters
To compare the perimeters, we need to compare the two fractions: $\frac{177}{20}$ (Perimeter of ∆ABE) and $\frac{47}{6}$ (Perimeter of rectangle BCDE).
We find a common denominator for 20 and 6. The LCM of 20 and 6 is 60.
Perimeter of ∆ABE = $\frac{177}{20} = \frac{177 \times 3}{20 \times 3} = \frac{531}{60}$ cm
Perimeter of rectangle BCDE = $\frac{47}{6} = \frac{47 \times 10}{6 \times 10} = \frac{470}{60}$ cm
Comparing the numerators, we see that $531 > 470$.
Therefore, $\frac{531}{60} > \frac{470}{60}$, which means $\frac{177}{20} > \frac{47}{6}$.
The perimeter of the triangle ABE is greater than the perimeter of the rectangle BCDE.
Question 6. Salil wants to put a picture in a frame. The picture is $7\frac{3}{5}$ cm wide. To fit in the frame the picture cannot be more than $7\frac{3}{10}$ cm wide. How much should the picture be trimmed?
Answer:
Solution:
Given:
Width of the picture = $7\frac{3}{5}$ cm.
Maximum allowed width for the frame = $7\frac{3}{10}$ cm.
To Find:
The amount by which the picture should be trimmed.
Solution:
To fit the picture in the frame, the width of the picture must be reduced from $7\frac{3}{5}$ cm to $7\frac{3}{10}$ cm.
The amount to be trimmed is the difference between the current width of the picture and the maximum allowed width for the frame.
Amount to be trimmed = Width of the picture - Maximum allowed width
= $7\frac{3}{5} - 7\frac{3}{10}$ cm.
First, convert the mixed numbers to improper fractions.
$7\frac{3}{5} = \frac{(7 \times 5) + 3}{5} = \frac{35 + 3}{5} = \frac{38}{5}$
$7\frac{3}{10} = \frac{(7 \times 10) + 3}{10} = \frac{70 + 3}{10} = \frac{73}{10}$
Now, subtract the improper fractions:
Amount to be trimmed = $\frac{38}{5} - \frac{73}{10}$
We need a common denominator for 5 and 10. The LCM of 5 and 10 is 10.
Convert $\frac{38}{5}$ to an equivalent fraction with denominator 10:
$\frac{38}{5} = \frac{38 \times 2}{5 \times 2} = \frac{76}{10}$
Now perform the subtraction:
Amount to be trimmed = $\frac{76}{10} - \frac{73}{10} = \frac{76 - 73}{10} = \frac{3}{10}$ cm.
Thus, the picture should be trimmed by $\mathbf{\frac{3}{10}}$ cm.
Question 7. Ritu ate $\frac{3}{5}$ part of an apple and the remaining apple was eaten by her brother Somu. How much part of the apple did Somu eat? Who had the larger share? By how much?
Answer:
Given:
Part of the apple eaten by Ritu = $\frac{3}{5}$
To Find:
1. The part of the apple eaten by Somu.
2. Who had the larger share.
3. By how much the larger share was greater.
Solution:
1. Part of the apple eaten by Somu:
Let the whole apple be represented by 1.
The part of the apple eaten by Somu is the remaining part after Ritu ate her share.
Part eaten by Somu = Total apple - Part eaten by Ritu
$= 1 - \frac{3}{5}$
To subtract, we can write 1 as $\frac{5}{5}$.
$= \frac{5}{5} - \frac{3}{5} = \frac{5 - 3}{5} = \frac{2}{5}$
So, Somu ate $\frac{2}{5}$ part of the apple.
2. Who had the larger share?
We need to compare the parts eaten by Ritu and Somu.
Ritu's share = $\frac{3}{5}$
Somu's share = $\frac{2}{5}$
Since the denominators are the same, we can compare the numerators. We see that $3 > 2$.
Therefore, $\frac{3}{5} > \frac{2}{5}$.
Ritu had the larger share.
3. By how much?
To find out by how much Ritu's share was larger, we subtract Somu's share from Ritu's share.
Difference = Ritu's share - Somu's share
$= \frac{3}{5} - \frac{2}{5} = \frac{3 - 2}{5} = \frac{1}{5}$
Ritu had a larger share by $\frac{1}{5}$ part of the apple.
Question 8. Michael finished colouring a picture in $\frac{7}{12}$ hour. Vaibhav finished colouring the same picture in $\frac{3}{4}$ hour. Who worked longer? By what fraction was it longer?
Answer:
Given:
Time taken by Michael = $\frac{7}{12}$ hour.
Time taken by Vaibhav = $\frac{3}{4}$ hour.
To Find:
Who worked longer, and by what fraction.
Solution:
To find who worked longer, we need to compare the time taken by Michael and Vaibhav. This involves comparing the fractions $\frac{7}{12}$ and $\frac{3}{4}$.
To compare these fractions, we find a common denominator. The denominators are 12 and 4.
The Least Common Multiple (LCM) of 12 and 4 is 12.
Convert the fraction $\frac{3}{4}$ to an equivalent fraction with denominator 12:
$\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}$
Now compare $\frac{7}{12}$ (Michael's time) and $\frac{9}{12}$ (Vaibhav's time).
Since the denominators are the same, we compare the numerators: 7 and 9.
$7 < 9$
So, $\frac{7}{12} < \frac{9}{12}$.
This means Michael took less time than Vaibhav.
Therefore, Vaibhav worked longer.
To find by what fraction Vaibhav worked longer, we subtract Michael's time from Vaibhav's time.
Difference in time = Vaibhav's time - Michael's time
Difference = $\frac{9}{12} - \frac{7}{12}$
Since the denominators are the same, we subtract the numerators:
Difference = $\frac{9 - 7}{12} = \frac{2}{12}$
We can simplify the fraction $\frac{2}{12}$ by dividing the numerator and the denominator by their greatest common divisor, which is 2.
$\frac{\cancel{2}^{1}}{\cancel{12}_{6}} = \frac{1}{6}$
So, the difference is $\frac{1}{6}$ hour.
Vaibhav worked longer by $\mathbf{\frac{1}{6}}$ hour.
Example 5 (Before Exercise 2.2)
Example 5 In a class of 40 students $\frac{1}{5}$ of the total number of studetns like to study English, $\frac{2}{5}$ of the total number like to study Mathematics and the remaining students like to study Science.
(i) How many students like to study English?
(ii) How many students like to study Mathematics?
(iii) What fraction of the total number of students like to study Science?
Answer:
Given:
Total number of students in the class = $40$.
Fraction of students who like English = $\frac{1}{5}$ of the total.
Fraction of students who like Mathematics = $\frac{2}{5}$ of the total.
Remaining students like Science.
To Find:
(i) Number of students who like English.
(ii) Number of students who like Mathematics.
(iii) Fraction of total students who like Science.
Solution:
(i) Number of students who like to study English:
Number of students who like English = $\frac{1}{5}$ of Total number of students
= $\frac{1}{5} \times 40$
= $\frac{1 \times 40}{5}$
= $\frac{40}{5}$
= $8$
So, 8 students like to study English.
(ii) Number of students who like to study Mathematics:
Number of students who like Mathematics = $\frac{2}{5}$ of Total number of students
= $\frac{2}{5} \times 40$
= $\frac{2 \times 40}{5}$
= $\frac{80}{5}$
= $16$
So, 16 students like to study Mathematics.
(iii) Fraction of the total number of students who like to study Science:
First, find the number of students who like Science.
Number of students who like Science = Total students - (Students who like English + Students who like Mathematics)
= $40 - (8 + 16)$
= $40 - 24$
= $16$
So, 16 students like to study Science.
Now, find the fraction of total students who like Science.
Fraction for Science = $\frac{\text{Number of students who like Science}}{\text{Total number of students}}$
= $\frac{16}{40}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor, which is 8.
= $\frac{16 \div 8}{40 \div 8} = \frac{2}{5}$
So, $\mathbf{\frac{2}{5}}$ of the total number of students like to study Science.
Exercise 2.2
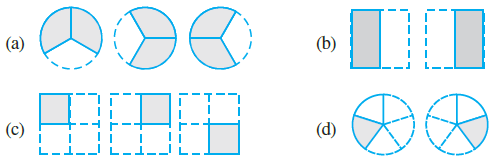
Question 1. Which of the drawings (a) to (d) show :
(i) $2 \times \frac{1}{5}$
(ii) $2 \times \frac{1}{2}$
(iii) $3 \times \frac{2}{3}$
(iv) $3 \times \frac{1}{4}$
Answer:
To match the mathematical expressions with the drawings, we need to interpret the multiplication of a whole number by a fraction. The expression "$a \times \frac{b}{c}$" can be read as "a groups of $\frac{b}{c}$".
(i) $2 \times \frac{1}{5}$
This expression represents two groups, where each group shows $\frac{1}{5}$. We need to look for a drawing that has two figures, each divided into 5 equal parts with 1 part shaded.
Drawing (d) shows two circles, each divided into 5 parts with 1 part shaded.
Therefore, (i) matches with (d).
(ii) $2 \times \frac{1}{2}$
This expression represents two groups, where each group shows $\frac{1}{2}$. We need to look for a drawing that has two figures, each divided into 2 equal parts with 1 part shaded.
Drawing (b) shows two rectangles, each divided into 2 parts with 1 part shaded.
Therefore, (ii) matches with (b).
(iii) $3 \times \frac{2}{3}$
This expression represents three groups, where each group shows $\frac{2}{3}$. We need to look for a drawing that has three figures, each divided into 3 equal parts with 2 parts shaded.
Drawing (a) shows three circles, each divided into 3 parts with 2 parts shaded.
Therefore, (iii) matches with (a).
(iv) $3 \times \frac{1}{4}$
This expression represents three groups, where each group shows $\frac{1}{4}$. We need to look for a drawing that has three figures, each divided into 4 equal parts with 1 part shaded.
Drawing (c) shows three squares, each divided into 4 parts with 1 part shaded.
Therefore, (iv) matches with (c).
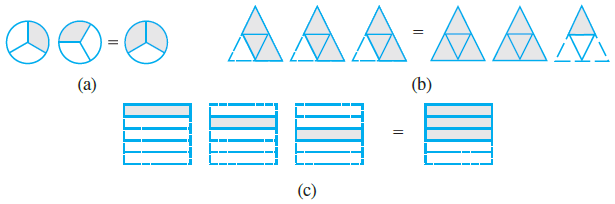
Question 2. Some pictures (a) to (c) are given below. Tell which of them show:
(i) $3 \times \frac{1}{5} = \frac{3}{5}$
(ii) $2 \times \frac{1}{3} = \frac{2}{3}$
(iii) $3 \times \frac{3}{4} = 2\frac{1}{4}$
Answer:
To match the pictures with the mathematical expressions, we need to analyze what each picture and expression represents.
(i) $3 \times \frac{1}{5} = \frac{3}{5}$
This expression shows 3 groups of $\frac{1}{5}$, which results in a total of $\frac{3}{5}$.
Picture (c) shows three figures, each with 1 out of 5 parts shaded ($3 \times \frac{1}{5}$). The result shown is a single figure with 3 out of 5 parts shaded ($\frac{3}{5}$).
Therefore, (i) matches with (c).
(ii) $2 \times \frac{1}{3} = \frac{2}{3}$
This expression shows 2 groups of $\frac{1}{3}$, which results in a total of $\frac{2}{3}$.
Picture (a) shows two figures, each with 1 out of 3 parts shaded ($2 \times \frac{1}{3}$). The result shown is a single figure with 2 out of 3 parts shaded ($\frac{2}{3}$).
Therefore, (ii) matches with (a).
(iii) $3 \times \frac{3}{4} = 2\frac{1}{4}$
This expression shows 3 groups of $\frac{3}{4}$, which results in a total of $\frac{9}{4}$ or $2\frac{1}{4}$.
Picture (b) shows three figures, each with 3 out of 4 parts shaded ($3 \times \frac{3}{4}$). The result shown is two fully shaded figures and one figure with 1 out of 4 parts shaded ($2\frac{1}{4}$).
Therefore, (iii) matches with (b).
Question 3. Multiply and reduce to lowest form and convert into a mixed fraction:
(i) $7 \times \frac{3}{5}$
(ii) $4 \times \frac{1}{3}$
(iii) $2 \times \frac{6}{7}$
(iv) $5 \times \frac{2}{9}$
(v) $\frac{2}{3} \times 4$
(vi) $\frac{5}{2} \times 6$
(vii) $11 \times \frac{4}{7}$
(viii) $20 \times \frac{4}{5}$
(ix) $13 \times \frac{1}{3}$
(x) $15 \times \frac{3}{5}$
Answer:
Solution:
(i) $7 \times \frac{3}{5}$
$7 \times \frac{3}{5} = \frac{7 \times 3}{5} = \frac{21}{5}$
This is an improper fraction. To convert it to a mixed fraction, divide 21 by 5.
$21 \div 5 = 4$ with remainder 1.
So, $\frac{21}{5} = 4\frac{1}{5}$.
The answer is $\mathbf{4\frac{1}{5}}$.
(ii) $4 \times \frac{1}{3}$
$4 \times \frac{1}{3} = \frac{4 \times 1}{3} = \frac{4}{3}$
This is an improper fraction. To convert it to a mixed fraction, divide 4 by 3.
$4 \div 3 = 1$ with remainder 1.
So, $\frac{4}{3} = 1\frac{1}{3}$.
The answer is $\mathbf{1\frac{1}{3}}$.
(iii) $2 \times \frac{6}{7}$
$2 \times \frac{6}{7} = \frac{2 \times 6}{7} = \frac{12}{7}$
This is an improper fraction. To convert it to a mixed fraction, divide 12 by 7.
$12 \div 7 = 1$ with remainder 5.
So, $\frac{12}{7} = 1\frac{5}{7}$.
The answer is $\mathbf{1\frac{5}{7}}$.
(iv) $5 \times \frac{2}{9}$
$5 \times \frac{2}{9} = \frac{5 \times 2}{9} = \frac{10}{9}$
This is an improper fraction. To convert it to a mixed fraction, divide 10 by 9.
$10 \div 9 = 1$ with remainder 1.
So, $\frac{10}{9} = 1\frac{1}{9}$.
The answer is $\mathbf{1\frac{1}{9}}$.
(v) $\frac{2}{3} \times 4$
$\frac{2}{3} \times 4 = \frac{2 \times 4}{3} = \frac{8}{3}$
This is an improper fraction. To convert it to a mixed fraction, divide 8 by 3.
$8 \div 3 = 2$ with remainder 2.
So, $\frac{8}{3} = 2\frac{2}{3}$.
The answer is $\mathbf{2\frac{2}{3}}$.
(vi) $\frac{5}{2} \times 6$
$\frac{5}{2} \times 6 = \frac{5 \times \cancel{6}^{3}}{\cancel{2}_{1}} = 5 \times 3 = 15$
The result is a whole number, $\mathbf{15}$.
(vii) $11 \times \frac{4}{7}$
$11 \times \frac{4}{7} = \frac{11 \times 4}{7} = \frac{44}{7}$
This is an improper fraction. To convert it to a mixed fraction, divide 44 by 7.
$44 \div 7 = 6$ with remainder 2.
So, $\frac{44}{7} = 6\frac{2}{7}$.
The answer is $\mathbf{6\frac{2}{7}}$.
(viii) $20 \times \frac{4}{5}$
$20 \times \frac{4}{5} = \frac{\cancel{20}^{4} \times 4}{\cancel{5}_{1}} = 4 \times 4 = 16$
The result is a whole number, $\mathbf{16}$.
(ix) $13 \times \frac{1}{3}$
$13 \times \frac{1}{3} = \frac{13 \times 1}{3} = \frac{13}{3}$
This is an improper fraction. To convert it to a mixed fraction, divide 13 by 3.
$13 \div 3 = 4$ with remainder 1.
So, $\frac{13}{3} = 4\frac{1}{3}$.
The answer is $\mathbf{4\frac{1}{3}}$.
(x) $15 \times \frac{3}{5}$
$15 \times \frac{3}{5} = \frac{\cancel{15}^{3} \times 3}{\cancel{5}_{1}} = 3 \times 3 = 9$
The result is a whole number, $\mathbf{9}$.
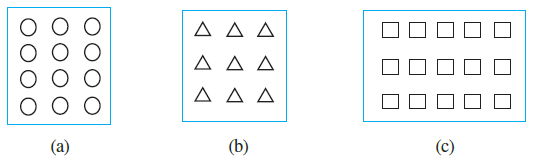
Question 4. Shade:
(i) $\frac{1}{2}$ of the circles in box (a)
(ii) $\frac{2}{3}$ of the triangles in box (b)
(iii) $\frac{3}{5}$ of the squares in box (c).
Answer:
(i) $\frac{1}{2}$ of the circles in box (a)
First, we count the total number of circles in box (a). There are 12 circles in total.
To find the number of circles to shade, we calculate $\frac{1}{2}$ of 12:
$\frac{1}{2} \times 12 = \frac{12}{2} = 6$
So, we need to shade 6 circles in box (a).
(ii) $\frac{2}{3}$ of the triangles in box (b)
First, we count the total number of triangles in box (b). There are 9 triangles in total.
To find the number of triangles to shade, we calculate $\frac{2}{3}$ of 9:
$\frac{2}{3} \times 9 = \frac{18}{3} = 6$
So, we need to shade 6 triangles in box (b).
(iii) $\frac{3}{5}$ of the squares in box (c)
First, we count the total number of squares in box (c). There are 15 squares in total.
To find the number of squares to shade, we calculate $\frac{3}{5}$ of 15:
$\frac{3}{5} \times 15 = \frac{45}{5} = 9$
So, we need to shade 9 squares in box (c).
Question 5. Find:
(a) $\frac{1}{2}$ of (i) 24 (ii) 46
(b) $\frac{2}{3}$ of (i) 18 (ii) 27
(c) $\frac{3}{4}$ of (i) 16 (ii) 36
(d) $\frac{4}{5}$ of (i) 20 (ii) 35
Answer:
Solution:
(a) $\frac{1}{2}$ of (i) 24 (ii) 46
(i) $\frac{1}{2}$ of 24 means $\frac{1}{2} \times 24$.
$\frac{1}{2} \times 24 = \frac{1 \times 24}{2} = \frac{24}{2} = 12$
So, $\frac{1}{2}$ of 24 is 12.
(ii) $\frac{1}{2}$ of 46 means $\frac{1}{2} \times 46$.
$\frac{1}{2} \times 46 = \frac{1 \times 46}{2} = \frac{46}{2} = 23$
So, $\frac{1}{2}$ of 46 is 23.
(b) $\frac{2}{3}$ of (i) 18 (ii) 27
(i) $\frac{2}{3}$ of 18 means $\frac{2}{3} \times 18$.
$\frac{2}{3} \times 18 = \frac{2 \times \cancel{18}^{6}}{\cancel{3}_{1}} = 2 \times 6 = 12$
So, $\frac{2}{3}$ of 18 is 12.
(ii) $\frac{2}{3}$ of 27 means $\frac{2}{3} \times 27$.
$\frac{2}{3} \times 27 = \frac{2 \times \cancel{27}^{9}}{\cancel{3}_{1}} = 2 \times 9 = 18$
So, $\frac{2}{3}$ of 27 is 18.
(c) $\frac{3}{4}$ of (i) 16 (ii) 36
(i) $\frac{3}{4}$ of 16 means $\frac{3}{4} \times 16$.
$\frac{3}{4} \times 16 = \frac{3 \times \cancel{16}^{4}}{\cancel{4}_{1}} = 3 \times 4 = 12$
So, $\frac{3}{4}$ of 16 is 12.
(ii) $\frac{3}{4}$ of 36 means $\frac{3}{4} \times 36$.
$\frac{3}{4} \times 36 = \frac{3 \times \cancel{36}^{9}}{\cancel{4}_{1}} = 3 \times 9 = 27$
So, $\frac{3}{4}$ of 36 is 27.
(d) $\frac{4}{5}$ of (i) 20 (ii) 35
(i) $\frac{4}{5}$ of 20 means $\frac{4}{5} \times 20$.
$\frac{4}{5} \times 20 = \frac{4 \times \cancel{20}^{4}}{\cancel{5}_{1}} = 4 \times 4 = 16$
So, $\frac{4}{5}$ of 20 is 16.
(ii) $\frac{4}{5}$ of 35 means $\frac{4}{5} \times 35$.
$\frac{4}{5} \times 35 = \frac{4 \times \cancel{35}^{7}}{\cancel{5}_{1}} = 4 \times 7 = 28$
So, $\frac{4}{5}$ of 35 is 28.
Question 6. Multiply and express as a mixed fraction :
(a) $3 \times 5\frac{1}{5}$
(b) $5 \times 6\frac{3}{4}$
(c) $7 \times 2\frac{1}{4}$
(d) $4 \times 6\frac{1}{3}$
(e) $3\frac{1}{4} \times 6$
(f) $3\frac{2}{5} \times 8$
Answer:
Solution:
(a) $3 \times 5\frac{1}{5}$
First, convert the mixed fraction to an improper fraction:
$5\frac{1}{5} = \frac{(5 \times 5) + 1}{5} = \frac{25 + 1}{5} = \frac{26}{5}$
Now, multiply the whole number by the improper fraction:
$3 \times \frac{26}{5} = \frac{3 \times 26}{5} = \frac{78}{5}$
Convert the improper fraction back to a mixed fraction. Divide 78 by 5:
$78 \div 5 = 15$ with a remainder of $3$.
So, $\frac{78}{5} = 15\frac{3}{5}$.
The answer is $\mathbf{15\frac{3}{5}}$.
(b) $5 \times 6\frac{3}{4}$
Convert the mixed fraction to an improper fraction:
$6\frac{3}{4} = \frac{(6 \times 4) + 3}{4} = \frac{24 + 3}{4} = \frac{27}{4}$
Now, multiply:
$5 \times \frac{27}{4} = \frac{5 \times 27}{4} = \frac{135}{4}$
Convert the improper fraction to a mixed fraction. Divide 135 by 4:
$135 \div 4 = 33$ with a remainder of $3$.
So, $\frac{135}{4} = 33\frac{3}{4}$.
The answer is $\mathbf{33\frac{3}{4}}$.
(c) $7 \times 2\frac{1}{4}$
Convert the mixed fraction to an improper fraction:
$2\frac{1}{4} = \frac{(2 \times 4) + 1}{4} = \frac{8 + 1}{4} = \frac{9}{4}$
Now, multiply:
$7 \times \frac{9}{4} = \frac{7 \times 9}{4} = \frac{63}{4}$
Convert the improper fraction to a mixed fraction. Divide 63 by 4:
$63 \div 4 = 15$ with a remainder of $3$.
So, $\frac{63}{4} = 15\frac{3}{4}$.
The answer is $\mathbf{15\frac{3}{4}}$.
(d) $4 \times 6\frac{1}{3}$
Convert the mixed fraction to an improper fraction:
$6\frac{1}{3} = \frac{(6 \times 3) + 1}{3} = \frac{18 + 1}{3} = \frac{19}{3}$
Now, multiply:
$4 \times \frac{19}{3} = \frac{4 \times 19}{3} = \frac{76}{3}$
Convert the improper fraction to a mixed fraction. Divide 76 by 3:
$76 \div 3 = 25$ with a remainder of $1$.
So, $\frac{76}{3} = 25\frac{1}{3}$.
The answer is $\mathbf{25\frac{1}{3}}$.
(e) $3\frac{1}{4} \times 6$
Convert the mixed fraction to an improper fraction:
$3\frac{1}{4} = \frac{(3 \times 4) + 1}{4} = \frac{12 + 1}{4} = \frac{13}{4}$
Now, multiply:
$\frac{13}{4} \times 6 = \frac{13 \times 6}{4}$
Simplify by canceling common factors:
$\frac{13 \times \cancel{6}^{3}}{\cancel{4}_{2}} = \frac{13 \times 3}{2} = \frac{39}{2}$
Convert the improper fraction to a mixed fraction. Divide 39 by 2:
$39 \div 2 = 19$ with a remainder of $1$.
So, $\frac{39}{2} = 19\frac{1}{2}$.
The answer is $\mathbf{19\frac{1}{2}}$.
(f) $3\frac{2}{5} \times 8$
Convert the mixed fraction to an improper fraction:
$3\frac{2}{5} = \frac{(3 \times 5) + 2}{5} = \frac{15 + 2}{5} = \frac{17}{5}$
Now, multiply:
$\frac{17}{5} \times 8 = \frac{17 \times 8}{5} = \frac{136}{5}$
Convert the improper fraction to a mixed fraction. Divide 136 by 5:
$136 \div 5 = 27$ with a remainder of $1$.
So, $\frac{136}{5} = 27\frac{1}{5}$.
The answer is $\mathbf{27\frac{1}{5}}$.
Question 7. Find:
(a) $\frac{1}{2}$ of (i) $2\frac{3}{4}$ (ii) $4\frac{2}{9}$
(b) $\frac{5}{8}$ of (i) $3\frac{5}{6}$ (ii) $9\frac{2}{3}$
Answer:
Solution:
(a) $\frac{1}{2}$ of (i) $2\frac{3}{4}$ (ii) $4\frac{2}{9}$
(i) We need to find $\frac{1}{2}$ of $2\frac{3}{4}$. This means multiplying $\frac{1}{2}$ by $2\frac{3}{4}$.
First, convert the mixed fraction $2\frac{3}{4}$ to an improper fraction:
$2\frac{3}{4} = \frac{(2 \times 4) + 3}{4} = \frac{8 + 3}{4} = \frac{11}{4}$
Now, multiply:
$\frac{1}{2} \times \frac{11}{4} = \frac{1 \times 11}{2 \times 4} = \frac{11}{8}$
Convert the improper fraction to a mixed fraction. Divide 11 by 8:
$11 \div 8 = 1$ with a remainder of $3$.
So, $\frac{11}{8} = 1\frac{3}{8}$.
$\frac{1}{2}$ of $2\frac{3}{4}$ is $\mathbf{1\frac{3}{8}}$.
(ii) We need to find $\frac{1}{2}$ of $4\frac{2}{9}$. This means multiplying $\frac{1}{2}$ by $4\frac{2}{9}$.
First, convert the mixed fraction $4\frac{2}{9}$ to an improper fraction:
$4\frac{2}{9} = \frac{(4 \times 9) + 2}{9} = \frac{36 + 2}{9} = \frac{38}{9}$
Now, multiply:
$\frac{1}{2} \times \frac{38}{9} = \frac{1 \times \cancel{38}^{19}}{\cancel{2}_{1} \times 9} = \frac{1 \times 19}{1 \times 9} = \frac{19}{9}$
Convert the improper fraction to a mixed fraction. Divide 19 by 9:
$19 \div 9 = 2$ with a remainder of $1$.
So, $\frac{19}{9} = 2\frac{1}{9}$.
$\frac{1}{2}$ of $4\frac{2}{9}$ is $\mathbf{2\frac{1}{9}}$.
(b) $\frac{5}{8}$ of (i) $3\frac{5}{6}$ (ii) $9\frac{2}{3}$
(i) We need to find $\frac{5}{8}$ of $3\frac{5}{6}$. This means multiplying $\frac{5}{8}$ by $3\frac{5}{6}$.
First, convert the mixed fraction $3\frac{5}{6}$ to an improper fraction:
$3\frac{5}{6} = \frac{(3 \times 6) + 5}{6} = \frac{18 + 5}{6} = \frac{23}{6}$
Now, multiply:
$\frac{5}{8} \times \frac{23}{6} = \frac{5 \times 23}{8 \times 6} = \frac{115}{48}$
Convert the improper fraction to a mixed fraction. Divide 115 by 48:
$115 \div 48 = 2$ with a remainder of $19$.
So, $\frac{115}{48} = 2\frac{19}{48}$.
$\frac{5}{8}$ of $3\frac{5}{6}$ is $\mathbf{2\frac{19}{48}}$.
(ii) We need to find $\frac{5}{8}$ of $9\frac{2}{3}$. This means multiplying $\frac{5}{8}$ by $9\frac{2}{3}$.
First, convert the mixed fraction $9\frac{2}{3}$ to an improper fraction:
$9\frac{2}{3} = \frac{(9 \times 3) + 2}{3} = \frac{27 + 2}{3} = \frac{29}{3}$
Now, multiply:
$\frac{5}{8} \times \frac{29}{3} = \frac{5 \times 29}{8 \times 3} = \frac{145}{24}$
Convert the improper fraction to a mixed fraction. Divide 145 by 24:
$145 \div 24 = 6$ with a remainder of $1$.
So, $\frac{145}{24} = 6\frac{1}{24}$.
$\frac{5}{8}$ of $9\frac{2}{3}$ is $\mathbf{6\frac{1}{24}}$.
Question 8. Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 litres of water. Vidya consumed $\frac{2}{5}$ of the water. Pratap consumed the remaining water.
(i) How much water did Vidya drink?
(ii) What fraction of the total quantity of water did Pratap drink?
Answer:
Solution:
Given:
Total quantity of water in the bottle = 5 litres.
Fraction of water consumed by Vidya = $\frac{2}{5}$ of the total water.
Pratap consumed the remaining water.
To Find:
(i) Amount of water Vidya drank (in litres).
(ii) Fraction of the total quantity of water Pratap drank.
Solution:
(i) How much water did Vidya drink?
Water consumed by Vidya = $\frac{2}{5}$ of 5 litres
= $\frac{2}{5} \times 5$ litres
= $\frac{2 \times 5}{5}$ litres
= $\frac{\cancel{10}^{2}}{\cancel{5}_{1}}$ litres
= $2$ litres.
So, Vidya drank $\mathbf{2}$ litres of water.
(ii) What fraction of the total quantity of water did Pratap drink?
The total quantity of water can be represented as a whole, which is 1.
Fraction of water consumed by Vidya = $\frac{2}{5}$.
The remaining fraction of water was consumed by Pratap.
Fraction of water consumed by Pratap = Total fraction - Fraction consumed by Vidya
= $1 - \frac{2}{5}$
To subtract the fraction from 1, we write 1 as a fraction with the same denominator (5).
$1 = \frac{5}{5}$
Fraction consumed by Pratap = $\frac{5}{5} - \frac{2}{5} = \frac{5 - 2}{5} = \frac{3}{5}$.
So, Pratap drank $\mathbf{\frac{3}{5}}$ fraction of the total quantity of water.
Alternatively, we can find the amount of water Pratap drank and then express it as a fraction of the total.
Water consumed by Pratap = Total water - Water consumed by Vidya
= $5$ litres - $2$ litres = $3$ litres.
Fraction of water consumed by Pratap = $\frac{\text{Water Pratap drank}}{\text{Total water}}$
= $\frac{3 \text{ litres}}{5 \text{ litres}} = \frac{3}{5}$.
Both methods give the same result.
Answers:
(i) Vidya drank $\mathbf{2}$ litres of water.
(ii) Pratap drank $\mathbf{\frac{3}{5}}$ fraction of the total quantity of water.
Example 6 (Before Exercise 2.3)
Example 6 Sushant reads $\frac{1}{3}$ part of a book in 1 hour. How much part of the book will he read in $2\frac{1}{5}$ hours?
Answer:
Solution:
Given:
Part of the book Sushant reads in 1 hour = $\frac{1}{3}$.
Time Sushant reads the book = $2\frac{1}{5}$ hours.
To Find:
How much part of the book Sushant will read in $2\frac{1}{5}$ hours.
Solution:
The part of the book read is equal to the reading rate (part per hour) multiplied by the time spent reading (in hours).
Part of book read = (Part read in 1 hour) $\times$ (Time in hours)
Part of book read = $\frac{1}{3} \times 2\frac{1}{5}$.
First, convert the mixed number $2\frac{1}{5}$ to an improper fraction:
$2\frac{1}{5} = \frac{(2 \times 5) + 1}{5} = \frac{10 + 1}{5} = \frac{11}{5}$ hours.
Now, multiply the fractions:
Part of book read = $\frac{1}{3} \times \frac{11}{5}$
To multiply fractions, multiply the numerators together and the denominators together:
Part of book read = $\frac{1 \times 11}{3 \times 5} = \frac{11}{15}$.
The fraction $\frac{11}{15}$ is in its lowest form because the only common factor of 11 and 15 is 1.
Thus, Sushant will read $\mathbf{\frac{11}{15}}$ part of the book in $2\frac{1}{5}$ hours.
Exercise 2.3
Question 1. Find:
(i) $\frac{1}{4}$ of (a) $\frac{1}{4}$ (b) $\frac{3}{5}$ (c) $\frac{4}{3}$
(ii) $\frac{1}{7}$ of (a) $\frac{2}{9}$ (b) $\frac{6}{5}$ (c) $\frac{3}{10}$
Answer:
Solution:
(i) $\frac{1}{4}$ of:
(a) $\frac{1}{4}$
This means $\frac{1}{4} \times \frac{1}{4}$.
$\frac{1}{4} \times \frac{1}{4} = \frac{1 \times 1}{4 \times 4} = \frac{1}{16}$
The fraction is already in its lowest form.
Answer: $\mathbf{\frac{1}{16}}$.
(b) $\frac{3}{5}$
This means $\frac{1}{4} \times \frac{3}{5}$.
$\frac{1}{4} \times \frac{3}{5} = \frac{1 \times 3}{4 \times 5} = \frac{3}{20}$
The fraction is already in its lowest form.
Answer: $\mathbf{\frac{3}{20}}$.
(c) $\frac{4}{3}$
This means $\frac{1}{4} \times \frac{4}{3}$.
$\frac{1}{4} \times \frac{4}{3} = \frac{1 \times \cancel{4}^{1}}{\cancel{4}_{1} \times 3} = \frac{1 \times 1}{1 \times 3} = \frac{1}{3}$
The fraction is already in its lowest form.
Answer: $\mathbf{\frac{1}{3}}$.
(ii) $\frac{1}{7}$ of:
(a) $\frac{2}{9}$
This means $\frac{1}{7} \times \frac{2}{9}$.
$\frac{1}{7} \times \frac{2}{9} = \frac{1 \times 2}{7 \times 9} = \frac{2}{63}$
The fraction is already in its lowest form.
Answer: $\mathbf{\frac{2}{63}}$.
(b) $\frac{6}{5}$
This means $\frac{1}{7} \times \frac{6}{5}$.
$\frac{1}{7} \times \frac{6}{5} = \frac{1 \times 6}{7 \times 5} = \frac{6}{35}$
The fraction is already in its lowest form.
Answer: $\mathbf{\frac{6}{35}}$.
(c) $\frac{3}{10}$
This means $\frac{1}{7} \times \frac{3}{10}$.
$\frac{1}{7} \times \frac{3}{10} = \frac{1 \times 3}{7 \times 10} = \frac{3}{70}$
The fraction is already in its lowest form.
Answer: $\mathbf{\frac{3}{70}}$.
Question 2. Multiply and reduce to lowest form (if possible) :
(i) $\frac{2}{3} \times 2\frac{2}{3}$
(ii) $\frac{2}{7} \times \frac{7}{9}$
(iii) $\frac{3}{8} \times \frac{6}{4}$
(iv) $\frac{9}{5} \times \frac{3}{5}$
(v) $\frac{1}{3} \times \frac{15}{8}$
(vi) $\frac{11}{2} \times \frac{3}{10}$
(vii) $\frac{4}{5} \times \frac{12}{7}$
Answer:
Solution:
(i) $\frac{2}{3} \times 2\frac{2}{3}$
First, convert the mixed fraction to an improper fraction:
$2\frac{2}{3} = \frac{(2 \times 3) + 2}{3} = \frac{6 + 2}{3} = \frac{8}{3}$
Now, multiply the fractions:
$\frac{2}{3} \times \frac{8}{3} = \frac{2 \times 8}{3 \times 3} = \frac{16}{9}$
The fraction $\frac{16}{9}$ is in its lowest form as 16 and 9 have no common factors other than 1.
Convert the improper fraction to a mixed fraction:
$16 \div 9 = 1$ with a remainder of $7$.
So, $\frac{16}{9} = 1\frac{7}{9}$.
The answer is $\mathbf{1\frac{7}{9}}$.
(ii) $\frac{2}{7} \times \frac{7}{9}$
Multiply the fractions:
$\frac{2}{7} \times \frac{7}{9} = \frac{2 \times 7}{7 \times 9}$
We can cancel the common factor 7:
$\frac{2 \times \cancel{7}^{1}}{\cancel{7}_{1} \times 9} = \frac{2 \times 1}{1 \times 9} = \frac{2}{9}$
The fraction $\frac{2}{9}$ is in its lowest form.
The answer is $\mathbf{\frac{2}{9}}$.
(iii) $\frac{3}{8} \times \frac{6}{4}$
Multiply the fractions:
$\frac{3}{8} \times \frac{6}{4} = \frac{3 \times 6}{8 \times 4}$
We can cancel common factors. 6 and 8 have a common factor of 2:
$\frac{3}{\cancel{8}_{4}} \times \frac{\cancel{6}^{3}}{4} = \frac{3 \times 3}{4 \times 4} = \frac{9}{16}$
The fraction $\frac{9}{16}$ is in its lowest form.
The answer is $\mathbf{\frac{9}{16}}$.
(iv) $\frac{9}{5} \times \frac{3}{5}$
Multiply the fractions:
$\frac{9}{5} \times \frac{3}{5} = \frac{9 \times 3}{5 \times 5} = \frac{27}{25}$
The fraction $\frac{27}{25}$ is in its lowest form.
Convert the improper fraction to a mixed fraction:
$27 \div 25 = 1$ with a remainder of $2$.
So, $\frac{27}{25} = 1\frac{2}{25}$.
The answer is $\mathbf{1\frac{2}{25}}$.
(v) $\frac{1}{3} \times \frac{15}{8}$
Multiply the fractions:
$\frac{1}{3} \times \frac{15}{8} = \frac{1 \times 15}{3 \times 8}$
We can cancel the common factor 3:
$\frac{1 \times \cancel{15}^{5}}{\cancel{3}_{1} \times 8} = \frac{1 \times 5}{1 \times 8} = \frac{5}{8}$
The fraction $\frac{5}{8}$ is in its lowest form.
The answer is $\mathbf{\frac{5}{8}}$.
(vi) $\frac{11}{2} \times \frac{3}{10}$
Multiply the fractions:
$\frac{11}{2} \times \frac{3}{10} = \frac{11 \times 3}{2 \times 10} = \frac{33}{20}$
The fraction $\frac{33}{20}$ is in its lowest form.
Convert the improper fraction to a mixed fraction:
$33 \div 20 = 1$ with a remainder of $13$.
So, $\frac{33}{20} = 1\frac{13}{20}$.
The answer is $\mathbf{1\frac{13}{20}}$.
(vii) $\frac{4}{5} \times \frac{12}{7}$
Multiply the fractions:
$\frac{4}{5} \times \frac{12}{7} = \frac{4 \times 12}{5 \times 7} = \frac{48}{35}$
The fraction $\frac{48}{35}$ is in its lowest form.
Convert the improper fraction to a mixed fraction:
$48 \div 35 = 1$ with a remainder of $13$.
So, $\frac{48}{35} = 1\frac{13}{35}$.
The answer is $\mathbf{1\frac{13}{35}}$.
Question 3. Multiply the following fractions:
(i) $\frac{2}{5} \times 5\frac{1}{4}$
(ii) $6\frac{2}{5} \times \frac{7}{9}$
(iii) $\frac{3}{2} \times 5\frac{1}{3}$
(iv) $\frac{5}{6} \times 2\frac{3}{7}$
(v) $3\frac{2}{5} \times \frac{4}{7}$
(vi) $2\frac{3}{5} \times 3$
(vii) $3\frac{4}{7} \times \frac{3}{5}$
Answer:
Solution:
(i) $\frac{2}{5} \times 5\frac{1}{4}$
Convert the mixed fraction to an improper fraction:
$5\frac{1}{4} = \frac{(5 \times 4) + 1}{4} = \frac{20 + 1}{4} = \frac{21}{4}$
Now, multiply the fractions:
$\frac{2}{5} \times \frac{21}{4} = \frac{\cancel{2}^{1} \times 21}{5 \times \cancel{4}_{2}} = \frac{1 \times 21}{5 \times 2} = \frac{21}{10}$
Convert the improper fraction to a mixed fraction:
$21 \div 10 = 2$ with a remainder of $1$.
So, $\frac{21}{10} = 2\frac{1}{10}$.
The answer is $\mathbf{2\frac{1}{10}}$.
(ii) $6\frac{2}{5} \times \frac{7}{9}$
Convert the mixed fraction to an improper fraction:
$6\frac{2}{5} = \frac{(6 \times 5) + 2}{5} = \frac{30 + 2}{5} = \frac{32}{5}$
Now, multiply the fractions:
$\frac{32}{5} \times \frac{7}{9} = \frac{32 \times 7}{5 \times 9} = \frac{224}{45}$
Convert the improper fraction to a mixed fraction:
$224 \div 45 = 4$ with a remainder of $44$.
So, $\frac{224}{45} = 4\frac{44}{45}$.
The answer is $\mathbf{4\frac{44}{45}}$.
(iii) $\frac{3}{2} \times 5\frac{1}{3}$
Convert the mixed fraction to an improper fraction:
$5\frac{1}{3} = \frac{(5 \times 3) + 1}{3} = \frac{15 + 1}{3} = \frac{16}{3}$
Now, multiply the fractions:
$\frac{3}{2} \times \frac{16}{3} = \frac{\cancel{3}^{1} \times \cancel{16}^{8}}{\cancel{2}_{1} \times \cancel{3}_{1}} = \frac{1 \times 8}{1 \times 1} = \frac{8}{1} = 8$
The answer is $\mathbf{8}$.
(iv) $\frac{5}{6} \times 2\frac{3}{7}$
Convert the mixed fraction to an improper fraction:
$2\frac{3}{7} = \frac{(2 \times 7) + 3}{7} = \frac{14 + 3}{7} = \frac{17}{7}$
Now, multiply the fractions:
$\frac{5}{6} \times \frac{17}{7} = \frac{5 \times 17}{6 \times 7} = \frac{85}{42}$
Convert the improper fraction to a mixed fraction:
$85 \div 42 = 2$ with a remainder of $1$.
So, $\frac{85}{42} = 2\frac{1}{42}$.
The answer is $\mathbf{2\frac{1}{42}}$.
(v) $3\frac{2}{5} \times \frac{4}{7}$
Convert the mixed fraction to an improper fraction:
$3\frac{2}{5} = \frac{(3 \times 5) + 2}{5} = \frac{15 + 2}{5} = \frac{17}{5}$
Now, multiply the fractions:
$\frac{17}{5} \times \frac{4}{7} = \frac{17 \times 4}{5 \times 7} = \frac{68}{35}$
Convert the improper fraction to a mixed fraction:
$68 \div 35 = 1$ with a remainder of $33$.
So, $\frac{68}{35} = 1\frac{33}{35}$.
The answer is $\mathbf{1\frac{33}{35}}$.
(vi) $2\frac{3}{5} \times 3$
Convert the mixed fraction to an improper fraction:
$2\frac{3}{5} = \frac{(2 \times 5) + 3}{5} = \frac{10 + 3}{5} = \frac{13}{5}$
Now, multiply the fraction by the whole number:
$\frac{13}{5} \times 3 = \frac{13 \times 3}{5} = \frac{39}{5}$
Convert the improper fraction to a mixed fraction:
$39 \div 5 = 7$ with a remainder of $4$.
So, $\frac{39}{5} = 7\frac{4}{5}$.
The answer is $\mathbf{7\frac{4}{5}}$.
(vii) $3\frac{4}{7} \times \frac{3}{5}$
Convert the mixed fraction to an improper fraction:
$3\frac{4}{7} = \frac{(3 \times 7) + 4}{7} = \frac{21 + 4}{7} = \frac{25}{7}$
Now, multiply the fractions:
$\frac{25}{7} \times \frac{3}{5} = \frac{\cancel{25}^{5} \times 3}{7 \times \cancel{5}_{1}} = \frac{5 \times 3}{7 \times 1} = \frac{15}{7}$
Convert the improper fraction to a mixed fraction:
$15 \div 7 = 2$ with a remainder of $1$.
So, $\frac{15}{7} = 2\frac{1}{7}$.
The answer is $\mathbf{2\frac{1}{7}}$.
Question 4. Which is greater:
(i) $\frac{2}{7}$ of $\frac{3}{4}$ or $\frac{3}{5}$ of $\frac{5}{8}$
(ii) $\frac{1}{2}$ of $\frac{6}{7}$ or $\frac{2}{3}$ of $\frac{3}{7}$
Answer:
Solution:
(i) Compare $\frac{2}{7}$ of $\frac{3}{4}$ and $\frac{3}{5}$ of $\frac{5}{8}$.
First, calculate the value of the first quantity: $\frac{2}{7}$ of $\frac{3}{4}$.
$\frac{2}{7}$ of $\frac{3}{4} = \frac{2}{7} \times \frac{3}{4} = \frac{\cancel{2}^{1} \times 3}{7 \times \cancel{4}_{2}} = \frac{1 \times 3}{7 \times 2} = \frac{3}{14}$.
Next, calculate the value of the second quantity: $\frac{3}{5}$ of $\frac{5}{8}$.
$\frac{3}{5}$ of $\frac{5}{8} = \frac{3}{5} \times \frac{5}{8} = \frac{3 \times \cancel{5}^{1}}{\cancel{5}_{1} \times 8} = \frac{3 \times 1}{1 \times 8} = \frac{3}{8}$.
Now, we need to compare $\frac{3}{14}$ and $\frac{3}{8}$.
Since the numerators are the same (both are 3), the fraction with the smaller denominator is greater.
Comparing the denominators 14 and 8, we have $8 < 14$.
So, $\frac{3}{8} > \frac{3}{14}$.
Thus, $\frac{3}{5}$ of $\frac{5}{8}$ is greater than $\frac{2}{7}$ of $\frac{3}{4}$.
Alternatively, we can find a common denominator for 14 and 8. LCM(14, 8) = 56.
$\frac{3}{14} = \frac{3 \times 4}{14 \times 4} = \frac{12}{56}$.
$\frac{3}{8} = \frac{3 \times 7}{8 \times 7} = \frac{21}{56}$.
Comparing $\frac{12}{56}$ and $\frac{21}{56}$, since $21 > 12$, we have $\frac{21}{56} > \frac{12}{56}$.
Therefore, $\frac{3}{8} > \frac{3}{14}$.
The quantity $\mathbf{\frac{3}{5} \text{ of } \frac{5}{8}}$ is greater.
(ii) Compare $\frac{1}{2}$ of $\frac{6}{7}$ and $\frac{2}{3}$ of $\frac{3}{7}$.
First, calculate the value of the first quantity: $\frac{1}{2}$ of $\frac{6}{7}$.
$\frac{1}{2}$ of $\frac{6}{7} = \frac{1}{2} \times \frac{6}{7} = \frac{1 \times \cancel{6}^{3}}{\cancel{2}_{1} \times 7} = \frac{1 \times 3}{1 \times 7} = \frac{3}{7}$.
Next, calculate the value of the second quantity: $\frac{2}{3}$ of $\frac{3}{7}$.
$\frac{2}{3}$ of $\frac{3}{7} = \frac{2}{3} \times \frac{3}{7} = \frac{2 \times \cancel{3}^{1}}{\cancel{3}_{1} \times 7} = \frac{2 \times 1}{1 \times 7} = \frac{2}{7}$.
Now, we need to compare $\frac{3}{7}$ and $\frac{2}{7}$.
Since the denominators are the same (both are 7), we compare the numerators.
Comparing the numerators 3 and 2, we have $3 > 2$.
So, $\frac{3}{7} > \frac{2}{7}$.
Thus, $\frac{1}{2}$ of $\frac{6}{7}$ is greater than $\frac{2}{3}$ of $\frac{3}{7}$.
The quantity $\mathbf{\frac{1}{2} \text{ of } \frac{6}{7}}$ is greater.
Question 5. Saili plants 4 saplings, in a row, in her garden. The distance between two adjacent saplings is $\frac{3}{4}$ m. Find the distance between the first and the last sapling.
Answer:
Solution:
Given:
Number of saplings planted = 4.
The saplings are planted in a row.
Distance between two adjacent saplings = $\frac{3}{4}$ m.
To Find:
The distance between the first and the last sapling.
Solution:
Let the saplings be denoted as S1, S2, S3, and S4.
They are planted in a row like this: S1 --- S2 --- S3 --- S4.
The distance between S1 and S2 is $\frac{3}{4}$ m.
The distance between S2 and S3 is $\frac{3}{4}$ m.
The distance between S3 and S4 is $\frac{3}{4}$ m.
There are 3 intervals between the 4 saplings.
Number of intervals = Number of saplings - 1 = $4 - 1 = 3$.
The total distance between the first and the last sapling is the sum of the lengths of these intervals.
Total distance = (Number of intervals) $\times$ (Distance between adjacent saplings)
Total distance = $3 \times \frac{3}{4}$ m.
Multiply the whole number by the fraction:
$3 \times \frac{3}{4} = \frac{3 \times 3}{4} = \frac{9}{4}$ m.
The distance is $\frac{9}{4}$ m.
We can convert this improper fraction to a mixed number:
Divide 9 by 4: $9 \div 4 = 2$ with a remainder of $1$.
So, $\frac{9}{4} = 2\frac{1}{4}$.
The distance between the first and the last sapling is $\mathbf{2\frac{1}{4}}$ m (or $\mathbf{\frac{9}{4}}$ m).
Question 6. Lipika reads a book for $1\frac{3}{4}$ hours everyday. She reads the entire book in 6 days. How many hours in all were required by her to read the book?
Answer:
Solution:
Given:
Time Lipika reads a book everyday = $1\frac{3}{4}$ hours.
Number of days taken to read the entire book = 6 days.
To Find:
Total hours required by her to read the book.
Solution:
The total time required to read the book is the product of the time read each day and the number of days.
Total time = (Time read everyday) $\times$ (Number of days)
Total time = $1\frac{3}{4} \times 6$ hours.
First, convert the mixed number $1\frac{3}{4}$ to an improper fraction:
$1\frac{3}{4} = \frac{(1 \times 4) + 3}{4} = \frac{4 + 3}{4} = \frac{7}{4}$ hours.
Now, multiply the improper fraction by the number of days:
Total time = $\frac{7}{4} \times 6$
Total time = $\frac{7 \times 6}{4}$
We can simplify the multiplication by cancelling the common factor 2:
Total time = $\frac{7 \times \cancel{6}^{3}}{\cancel{4}_{2}} = \frac{7 \times 3}{2} = \frac{21}{2}$
The total time is $\frac{21}{2}$ hours.
We can convert this improper fraction to a mixed number by dividing the numerator by the denominator:
$21 \div 2 = 10$ with a remainder of $1$.
So, $\frac{21}{2} = 10\frac{1}{2}$.
Thus, the total hours required by Lipika to read the book were $\mathbf{10\frac{1}{2}}$ hours.
Question 7. A car runs 16 km using 1 litre of petrol. How much distance will it cover using $2\frac{3}{4}$ litres of petrol.
Answer:
Solution:
Given:
Distance covered by the car using 1 litre of petrol = $16$ km.
Quantity of petrol used = $2\frac{3}{4}$ litres.
To Find:
Total distance covered by the car using $2\frac{3}{4}$ litres of petrol.
Solution:
The total distance covered is the product of the distance covered per litre and the total quantity of petrol used.
Total distance = (Distance per litre) $\times$ (Quantity of petrol)
Total distance = $16 \times 2\frac{3}{4}$ km.
First, convert the mixed number $2\frac{3}{4}$ to an improper fraction:
$2\frac{3}{4} = \frac{(2 \times 4) + 3}{4} = \frac{8 + 3}{4} = \frac{11}{4}$ litres.
Now, multiply the distance per litre by the improper fraction:
Total distance = $16 \times \frac{11}{4}$ km.
Total distance = $\frac{16 \times 11}{4}$
We can simplify this by cancelling the common factor 4 from the numerator and the denominator:
Total distance = $\frac{\cancel{16}^{4} \times 11}{\cancel{4}_{1}} = \frac{4 \times 11}{1} = 4 \times 11 = 44$.
The total distance covered by the car is 44 km.
Thus, the car will cover a distance of $\mathbf{44}$ km using $2\frac{3}{4}$ litres of petrol.
Question 8.
(a) (i) Provide the number in the box ⬜ , such that $\frac{2}{3} \times ⬜ = \frac{10}{30}$ .
(ii) The simplest form of the number obtained in ⬜ is _____.
(b) (i) Provide the number in the box ⬜ , such that $\frac{3}{5} \times ⬜ = \frac{24}{75}$ .
(ii) The simplest form of the number obtained in ⬜ is _____.
Answer:
(a) (i) Provide the number in the box ⬜ , such that $\frac{2}{3} \times ⬜ = \frac{10}{30}$ .
Let the number in the box be a fraction $\frac{N}{D}$. The equation is:
$\frac{2}{3} \times \frac{N}{D} = \frac{10}{30}$
This implies $\frac{2 \times N}{3 \times D} = \frac{10}{30}$.
By comparing the numerators and denominators, we get:
For the numerator: $2 \times N = 10 \implies N = \frac{10}{2} = 5$.
For the denominator: $3 \times D = 30 \implies D = \frac{30}{3} = 10$.
So, the number in the box is $\frac{5}{10}$.
Therefore, $\frac{2}{3} \times \frac{5}{10} = \frac{10}{30}$.
(ii) The simplest form of the number obtained in ⬜ is _____.
The number obtained in the box is $\frac{5}{10}$.
To find its simplest form, we divide the numerator and the denominator by their greatest common divisor, which is 5.
$\frac{5 \div 5}{10 \div 5} = \frac{1}{2}$
The simplest form is $\frac{1}{2}$.
(b) (i) Provide the number in the box ⬜ , such that $\frac{3}{5} \times ⬜ = \frac{24}{75}$ .
Let the number in the box be a fraction $\frac{N}{D}$. The equation is:
$\frac{3}{5} \times \frac{N}{D} = \frac{24}{75}$
This implies $\frac{3 \times N}{5 \times D} = \frac{24}{75}$.
By comparing the numerators and denominators, we get:
For the numerator: $3 \times N = 24 \implies N = \frac{24}{3} = 8$.
For the denominator: $5 \times D = 75 \implies D = \frac{75}{5} = 15$.
So, the number in the box is $\frac{8}{15}$.
Therefore, $\frac{3}{5} \times \frac{8}{15} = \frac{24}{75}$.
(ii) The simplest form of the number obtained in ⬜ is _____.
The number obtained in the box is $\frac{8}{15}$.
To find its simplest form, we look for the greatest common divisor of 8 and 15. The factors of 8 are 1, 2, 4, 8. The factors of 15 are 1, 3, 5, 15. The only common factor is 1.
Since the greatest common divisor is 1, the fraction is already in its simplest form.
The simplest form is $\frac{8}{15}$.
Exercise 2.4
Question 1. Find:
(i) $12 \div \frac{3}{4}$
(ii) $14 \div \frac{5}{6}$
(iii) $8 \div \frac{7}{3}$
(iv) $4 \div\frac{8}{3}$
(v) $3 \div 2\frac{1}{3}$
(vi) $5 \div 3\frac{4}{7}$
Answer:
Solution:
(i) $12 \div \frac{3}{4}$
To divide a whole number by a fraction, multiply the whole number by the reciprocal of the fraction.
The reciprocal of $\frac{3}{4}$ is $\frac{4}{3}$.
$12 \div \frac{3}{4} = 12 \times \frac{4}{3}$
$= \frac{\cancel{12}^{4}}{1} \times \frac{4}{\cancel{3}_{1}}$
$= \frac{4 \times 4}{1 \times 1} = \frac{16}{1} = 16$
The answer is $\mathbf{16}$.
(ii) $14 \div \frac{5}{6}$
Multiply by the reciprocal of $\frac{5}{6}$, which is $\frac{6}{5}$.
$14 \div \frac{5}{6} = 14 \times \frac{6}{5}$
$= \frac{14 \times 6}{5} = \frac{84}{5}$
Convert the improper fraction to a mixed fraction:
$84 \div 5 = 16$ with a remainder of $4$.
So, $\frac{84}{5} = 16\frac{4}{5}$.
The answer is $\mathbf{16\frac{4}{5}}$.
(iii) $8 \div \frac{7}{3}$
Multiply by the reciprocal of $\frac{7}{3}$, which is $\frac{3}{7}$.
$8 \div \frac{7}{3} = 8 \times \frac{3}{7}$
$= \frac{8 \times 3}{7} = \frac{24}{7}$
Convert the improper fraction to a mixed fraction:
$24 \div 7 = 3$ with a remainder of $3$.
So, $\frac{24}{7} = 3\frac{3}{7}$.
The answer is $\mathbf{3\frac{3}{7}}$.
(iv) $4 \div\frac{8}{3}$
Multiply by the reciprocal of $\frac{8}{3}$, which is $\frac{3}{8}$.
$4 \div \frac{8}{3} = 4 \times \frac{3}{8}$
$= \frac{\cancel{4}^{1}}{1} \times \frac{3}{\cancel{8}_{2}}$
$= \frac{1 \times 3}{1 \times 2} = \frac{3}{2}$
Convert the improper fraction to a mixed fraction:
$3 \div 2 = 1$ with a remainder of $1$.
So, $\frac{3}{2} = 1\frac{1}{2}$.
The answer is $\mathbf{1\frac{1}{2}}$.
(v) $3 \div 2\frac{1}{3}$
First, convert the mixed number $2\frac{1}{3}$ to an improper fraction:
$2\frac{1}{3} = \frac{(2 \times 3) + 1}{3} = \frac{6 + 1}{3} = \frac{7}{3}$
Now, perform the division: $3 \div \frac{7}{3}$.
Multiply by the reciprocal of $\frac{7}{3}$, which is $\frac{3}{7}$.
$3 \times \frac{3}{7} = \frac{3 \times 3}{7} = \frac{9}{7}$
Convert the improper fraction to a mixed fraction:
$9 \div 7 = 1$ with a remainder of $2$.
So, $\frac{9}{7} = 1\frac{2}{7}$.
The answer is $\mathbf{1\frac{2}{7}}$.
(vi) $5 \div 3\frac{4}{7}$
First, convert the mixed number $3\frac{4}{7}$ to an improper fraction:
$3\frac{4}{7} = \frac{(3 \times 7) + 4}{7} = \frac{21 + 4}{7} = \frac{25}{7}$
Now, perform the division: $5 \div \frac{25}{7}$.
Multiply by the reciprocal of $\frac{25}{7}$, which is $\frac{7}{25}$.
$5 \times \frac{7}{25} = \frac{\cancel{5}^{1}}{1} \times \frac{7}{\cancel{25}_{5}}$
$= \frac{1 \times 7}{1 \times 5} = \frac{7}{5}$
Convert the improper fraction to a mixed fraction:
$7 \div 5 = 1$ with a remainder of $2$.
So, $\frac{7}{5} = 1\frac{2}{5}$.
The answer is $\mathbf{1\frac{2}{5}}$.
Question 2. Find the reciprocal of each of the following fractions. Classify the reciprocals as proper fractions, improper fractions and whole numbers.
(i) $\frac{3}{7}$
(ii) $\frac{5}{8}$
(iii) $\frac{9}{7}$
(iv) $\frac{6}{5}$
(v) $\frac{12}{7}$
(vi) $\frac{1}{8}$
(vii) $\frac{1}{11}$
Answer:
Solution:
The reciprocal of a fraction $\frac{a}{b}$ is $\frac{b}{a}$, where $a \neq 0$ and $b \neq 0$.
A fraction is classified as:
- Proper fraction: Numerator < Denominator
- Improper fraction: Numerator $\geq$ Denominator
- Whole number: An improper fraction that simplifies to an integer (i.e., numerator is a multiple of the denominator, and the denominator is 1).
(i) Fraction: $\frac{3}{7}$
Reciprocal: $\frac{7}{3}$
Classification: Since the numerator (7) is greater than the denominator (3), it is an $\mathbf{improper\ fraction}$.
(ii) Fraction: $\frac{5}{8}$
Reciprocal: $\frac{8}{5}$
Classification: Since the numerator (8) is greater than the denominator (5), it is an $\mathbf{improper\ fraction}$.
(iii) Fraction: $\frac{9}{7}$
Reciprocal: $\frac{7}{9}$
Classification: Since the numerator (7) is less than the denominator (9), it is a $\mathbf{proper\ fraction}$.
(iv) Fraction: $\frac{6}{5}$
Reciprocal: $\frac{5}{6}$
Classification: Since the numerator (5) is less than the denominator (6), it is a $\mathbf{proper\ fraction}$.
(v) Fraction: $\frac{12}{7}$
Reciprocal: $\frac{7}{12}$
Classification: Since the numerator (7) is less than the denominator (12), it is a $\mathbf{proper\ fraction}$.
(vi) Fraction: $\frac{1}{8}$
Reciprocal: $\frac{8}{1} = 8$
Classification: Since the reciprocal is 8, it is a $\mathbf{whole\ number}$.
(vii) Fraction: $\frac{1}{11}$
Reciprocal: $\frac{11}{1} = 11$
Classification: Since the reciprocal is 11, it is a $\mathbf{whole\ number}$.
Question 3. Find:
(i) $\frac{7}{3} \div 2$
(ii) $\frac{4}{9} \div 5$
(iii) $\frac{6}{13} \div 7$
(iv) $4\frac{1}{3} \div 3$
(v) $3\frac{1}{2} \div 4$
(vi) $4\frac{3}{7} \div 7$
Answer:
Solution:
(i) $\frac{7}{3} \div 2$
To divide a fraction by a whole number, we multiply the fraction by the reciprocal of the whole number. The whole number 2 can be written as $\frac{2}{1}$. The reciprocal of $\frac{2}{1}$ is $\frac{1}{2}$.
$\frac{7}{3} \div 2 = \frac{7}{3} \times \frac{1}{2}$
Multiply the numerators and the denominators:
$\frac{7 \times 1}{3 \times 2} = \frac{7}{6}$
This is an improper fraction. Convert it to a mixed fraction:
$7 \div 6 = 1$ with a remainder of $1$.
So, $\frac{7}{6} = 1\frac{1}{6}$.
The answer is $\mathbf{1\frac{1}{6}}$.
(ii) $\frac{4}{9} \div 5$
To divide the fraction by the whole number 5 (or $\frac{5}{1}$), multiply by the reciprocal of 5, which is $\frac{1}{5}$.
$\frac{4}{9} \div 5 = \frac{4}{9} \times \frac{1}{5}$
Multiply the numerators and the denominators:
$\frac{4 \times 1}{9 \times 5} = \frac{4}{45}$
This is a proper fraction and is in its lowest form.
The answer is $\mathbf{\frac{4}{45}}$.
(iii) $\frac{6}{13} \div 7$
To divide the fraction by the whole number 7 (or $\frac{7}{1}$), multiply by the reciprocal of 7, which is $\frac{1}{7}$.
$\frac{6}{13} \div 7 = \frac{6}{13} \times \frac{1}{7}$
Multiply the numerators and the denominators:
$\frac{6 \times 1}{13 \times 7} = \frac{6}{91}$
This is a proper fraction and is in its lowest form.
The answer is $\mathbf{\frac{6}{91}}$.
(iv) $4\frac{1}{3} \div 3$
First, convert the mixed number $4\frac{1}{3}$ to an improper fraction:
$4\frac{1}{3} = \frac{(4 \times 3) + 1}{3} = \frac{12 + 1}{3} = \frac{13}{3}$
Now, divide the improper fraction by the whole number 3 (or $\frac{3}{1}$). Multiply by the reciprocal of 3, which is $\frac{1}{3}$.
$\frac{13}{3} \div 3 = \frac{13}{3} \times \frac{1}{3}$
Multiply the numerators and the denominators:
$\frac{13 \times 1}{3 \times 3} = \frac{13}{9}$
This is an improper fraction. Convert it to a mixed fraction:
$13 \div 9 = 1$ with a remainder of $4$.
So, $\frac{13}{9} = 1\frac{4}{9}$.
The answer is $\mathbf{1\frac{4}{9}}$.
(v) $3\frac{1}{2} \div 4$
First, convert the mixed number $3\frac{1}{2}$ to an improper fraction:
$3\frac{1}{2} = \frac{(3 \times 2) + 1}{2} = \frac{6 + 1}{2} = \frac{7}{2}$
Now, divide the improper fraction by the whole number 4 (or $\frac{4}{1}$). Multiply by the reciprocal of 4, which is $\frac{1}{4}$.
$\frac{7}{2} \div 4 = \frac{7}{2} \times \frac{1}{4}$
Multiply the numerators and the denominators:
$\frac{7 \times 1}{2 \times 4} = \frac{7}{8}$
This is a proper fraction and is in its lowest form.
The answer is $\mathbf{\frac{7}{8}}$.
(vi) $4\frac{3}{7} \div 7$
First, convert the mixed number $4\frac{3}{7}$ to an improper fraction:
$4\frac{3}{7} = \frac{(4 \times 7) + 3}{7} = \frac{28 + 3}{7} = \frac{31}{7}$
Now, divide the improper fraction by the whole number 7 (or $\frac{7}{1}$). Multiply by the reciprocal of 7, which is $\frac{1}{7}$.
$\frac{31}{7} \div 7 = \frac{31}{7} \times \frac{1}{7}$
Multiply the numerators and the denominators:
$\frac{31 \times 1}{7 \times 7} = \frac{31}{49}$
This is a proper fraction and is in its lowest form.
The answer is $\mathbf{\frac{31}{49}}$.
Question 4. Find:
(i) $\frac{2}{5}\div\frac{1}{2}$
(ii) $\frac{4}{9}\div\frac{2}{3}$
(iii) $\frac{3}{7}\div\frac{8}{7}$
(iv) $2\frac{1}{3}\div\frac{3}{5}$
(v) $3\frac{1}{2}\div\frac{8}{3}$
(vi) $\frac{2}{5} \div 1\frac{1}{2}$
(vii) $3\frac{1}{5}\div 1\frac{2}{3}$
(viii) $2\frac{1}{5}\div 1\frac{1}{5}$
Answer:
Solution:
To divide a fraction by another fraction, we multiply the first fraction by the reciprocal of the second fraction.
(i) $\frac{2}{5}\div\frac{1}{2}$
The reciprocal of $\frac{1}{2}$ is $\frac{2}{1}$.
$\frac{2}{5} \div \frac{1}{2} = \frac{2}{5} \times \frac{2}{1}$
$= \frac{2 \times 2}{5 \times 1} = \frac{4}{5}$
The answer is $\mathbf{\frac{4}{5}}$.
(ii) $\frac{4}{9}\div\frac{2}{3}$
The reciprocal of $\frac{2}{3}$ is $\frac{3}{2}$.
$\frac{4}{9} \div \frac{2}{3} = \frac{4}{9} \times \frac{3}{2}$
$= \frac{\cancel{4}^{2} \times \cancel{3}^{1}}{\cancel{9}_{3} \times \cancel{2}_{1}} = \frac{2 \times 1}{3 \times 1} = \frac{2}{3}$
The answer is $\mathbf{\frac{2}{3}}$.
(iii) $\frac{3}{7}\div\frac{8}{7}$
The reciprocal of $\frac{8}{7}$ is $\frac{7}{8}$.
$\frac{3}{7} \div \frac{8}{7} = \frac{3}{7} \times \frac{7}{8}$
$= \frac{3 \times \cancel{7}^{1}}{\cancel{7}_{1} \times 8} = \frac{3 \times 1}{1 \times 8} = \frac{3}{8}$
The answer is $\mathbf{\frac{3}{8}}$.
(iv) $2\frac{1}{3}\div\frac{3}{5}$
First, convert the mixed number $2\frac{1}{3}$ to an improper fraction:
$2\frac{1}{3} = \frac{(2 \times 3) + 1}{3} = \frac{6 + 1}{3} = \frac{7}{3}$
Now, divide $\frac{7}{3}$ by $\frac{3}{5}$. The reciprocal of $\frac{3}{5}$ is $\frac{5}{3}$.
$\frac{7}{3} \div \frac{3}{5} = \frac{7}{3} \times \frac{5}{3}$
$= \frac{7 \times 5}{3 \times 3} = \frac{35}{9}$
Convert the improper fraction to a mixed fraction:
$35 \div 9 = 3$ with a remainder of $8$.
So, $\frac{35}{9} = 3\frac{8}{9}$.
The answer is $\mathbf{3\frac{8}{9}}$.
(v) $3\frac{1}{2}\div\frac{8}{3}$
First, convert the mixed number $3\frac{1}{2}$ to an improper fraction:
$3\frac{1}{2} = \frac{(3 \times 2) + 1}{2} = \frac{6 + 1}{2} = \frac{7}{2}$
Now, divide $\frac{7}{2}$ by $\frac{8}{3}$. The reciprocal of $\frac{8}{3}$ is $\frac{3}{8}$.
$\frac{7}{2} \div \frac{8}{3} = \frac{7}{2} \times \frac{3}{8}$
$= \frac{7 \times 3}{2 \times 8} = \frac{21}{16}$
Convert the improper fraction to a mixed fraction:
$21 \div 16 = 1$ with a remainder of $5$.
So, $\frac{21}{16} = 1\frac{5}{16}$.
The answer is $\mathbf{1\frac{5}{16}}$.
(vi) $\frac{2}{5} \div 1\frac{1}{2}$
First, convert the mixed number $1\frac{1}{2}$ to an improper fraction:
$1\frac{1}{2} = \frac{(1 \times 2) + 1}{2} = \frac{2 + 1}{2} = \frac{3}{2}$
Now, divide $\frac{2}{5}$ by $\frac{3}{2}$. The reciprocal of $\frac{3}{2}$ is $\frac{2}{3}$.
$\frac{2}{5} \div \frac{3}{2} = \frac{2}{5} \times \frac{2}{3}$
$= \frac{2 \times 2}{5 \times 3} = \frac{4}{15}$
The answer is $\mathbf{\frac{4}{15}}$.
(vii) $3\frac{1}{5}\div 1\frac{2}{3}$
First, convert both mixed numbers to improper fractions:
$3\frac{1}{5} = \frac{(3 \times 5) + 1}{5} = \frac{15 + 1}{5} = \frac{16}{5}$
$1\frac{2}{3} = \frac{(1 \times 3) + 2}{3} = \frac{3 + 2}{3} = \frac{5}{3}$
Now, divide $\frac{16}{5}$ by $\frac{5}{3}$. The reciprocal of $\frac{5}{3}$ is $\frac{3}{5}$.
$\frac{16}{5} \div \frac{5}{3} = \frac{16}{5} \times \frac{3}{5}$
$= \frac{16 \times 3}{5 \times 5} = \frac{48}{25}$
Convert the improper fraction to a mixed fraction:
$48 \div 25 = 1$ with a remainder of $23$.
So, $\frac{48}{25} = 1\frac{23}{25}$.
The answer is $\mathbf{1\frac{23}{25}}$.
(viii) $2\frac{1}{5}\div 1\frac{1}{5}$
First, convert both mixed numbers to improper fractions:
$2\frac{1}{5} = \frac{(2 \times 5) + 1}{5} = \frac{10 + 1}{5} = \frac{11}{5}$
$1\frac{1}{5} = \frac{(1 \times 5) + 1}{5} = \frac{5 + 1}{5} = \frac{6}{5}$
Now, divide $\frac{11}{5}$ by $\frac{6}{5}$. The reciprocal of $\frac{6}{5}$ is $\frac{5}{6}$.
$\frac{11}{5} \div \frac{6}{5} = \frac{11}{5} \times \frac{5}{6}$
$= \frac{11 \times \cancel{5}^{1}}{\cancel{5}_{1} \times 6} = \frac{11 \times 1}{1 \times 6} = \frac{11}{6}$
Convert the improper fraction to a mixed fraction:
$11 \div 6 = 1$ with a remainder of $5$.
So, $\frac{11}{6} = 1\frac{5}{6}$.
The answer is $\mathbf{1\frac{5}{6}}$.
Exercise 2.5
Question 1. Which is greater?
(i) 0.5 or 0.05
(ii) 0.7 or 0.5
(iii) 7 or 0.7
(iv) 1.37 or 1.49
(v) 2.03 or 2.30
(vi) 0.8 or 0.88.
Answer:
Solution:
To determine which decimal number is greater, we compare the digits from left to right, starting from the highest place value (the whole number part), then the tenths, hundredths, and so on.
(i) Comparing $0.5$ and $0.05$.
Whole number part: $0 = 0$.
Tenths place: $5 > 0$.
Since $5 > 0$ at the tenths place, $0.5$ is greater than $0.05$.
So, $\mathbf{0.5}$ is greater.
(ii) Comparing $0.7$ and $0.5$.
Whole number part: $0 = 0$.
Tenths place: $7 > 5$.
Since $7 > 5$ at the tenths place, $0.7$ is greater than $0.5$.
So, $\mathbf{0.7}$ is greater.
(iii) Comparing $7$ and $0.7$.
We can write $7$ as $7.0$.
Whole number part: $7 > 0$.
Since $7 > 0$ at the whole number place, $7$ is greater than $0.7$.
So, $\mathbf{7}$ is greater.
(iv) Comparing $1.37$ and $1.49$.
Whole number part: $1 = 1$.
Tenths place: $3 < 4$.
Since $3 < 4$ at the tenths place, $1.49$ is greater than $1.37$.
So, $\mathbf{1.49}$ is greater.
(v) Comparing $2.03$ and $2.30$.
Whole number part: $2 = 2$.
Tenths place: $0 < 3$.
Since $0 < 3$ at the tenths place, $2.30$ is greater than $2.03$.
So, $\mathbf{2.30}$ is greater.
(vi) Comparing $0.8$ and $0.88$.
We can write $0.8$ as $0.80$.
Whole number part: $0 = 0$.
Tenths place: $8 = 8$.
Hundredths place: $0 < 8$.
Since $0 < 8$ at the hundredths place, $0.88$ is greater than $0.80$.
So, $\mathbf{0.88}$ is greater.
Question 2. Express as rupees using decimals :
(i) 7 paise
(ii) 7 rupees 7 paise
(iii) 77 rupees 77 paise
(iv) 50 paise
(v) 235 paise.
Answer:
Solution:
We know that $1$ Rupee = $100$ paise.
Therefore, $1$ paise = $\frac{1}{100}$ Rupee.
To convert paise to rupees, we divide the number of paise by 100.
(i) 7 paise
7 paise = $\frac{7}{100}$ $\textsf{₹}$
As a decimal, $\frac{7}{100} = 0.07$.
So, 7 paise = $\mathbf{\textsf{₹}0.07}$.
(ii) 7 rupees 7 paise
7 rupees 7 paise = 7 rupees + 7 paise
Convert 7 paise to rupees: 7 paise = $\frac{7}{100}$ $\textsf{₹} = 0.07$ $\textsf{₹}$.
Total amount = $7$ $\textsf{₹} + 0.07$ $\textsf{₹} = \mathbf{\textsf{₹}7.07}$.
(iii) 77 rupees 77 paise
77 rupees 77 paise = 77 rupees + 77 paise
Convert 77 paise to rupees: 77 paise = $\frac{77}{100}$ $\textsf{₹} = 0.77$ $\textsf{₹}$.
Total amount = $77$ $\textsf{₹} + 0.77$ $\textsf{₹} = \mathbf{\textsf{₹}77.77}$.
(iv) 50 paise
50 paise = $\frac{50}{100}$ $\textsf{₹}$
As a decimal, $\frac{50}{100} = 0.50$.
So, 50 paise = $\mathbf{\textsf{₹}0.50}$.
(v) 235 paise
235 paise = $\frac{235}{100}$ $\textsf{₹}$
As a decimal, $\frac{235}{100} = 2.35$.
So, 235 paise = $\mathbf{\textsf{₹}2.35}$.
Question 3.
(i) Express 5 cm in metre and kilometre
(ii) Express 35 mm in cm, m and km
Answer:
Solution:
We use the following conversion factors:
$1$ m $= 100$ cm
$1$ km $= 1000$ m
$1$ cm $= 10$ mm
From these, we get:
$1$ cm $= \frac{1}{100}$ m $= 0.01$ m
$1$ m $= \frac{1}{1000}$ km $= 0.001$ km
$1$ cm $= \frac{1}{10}$ mm $= 0.1$ cm
$1$ mm $= \frac{1}{10}$ cm $= 0.1$ cm
$1$ mm $= \frac{1}{1000}$ m $= 0.001$ m
$1$ mm $= \frac{1}{1000 \times 1000}$ km $= \frac{1}{1000000}$ km $= 0.000001$ km
(i) Express 5 cm in metre and kilometre
To express 5 cm in metres, we divide 5 by 100:
$5 \text{ cm} = \frac{5}{100} \text{ m} = \mathbf{0.05 \text{ m}}$
To express 5 cm in kilometres, we first convert it to metres (which is 0.05 m) and then convert metres to kilometres by dividing by 1000:
$5 \text{ cm} = 0.05 \text{ m} = \frac{0.05}{1000} \text{ km}$
$= 0.05 \times 0.001 \text{ km} = \mathbf{0.00005 \text{ km}}$
(ii) Express 35 mm in cm, m and km
To express 35 mm in centimetres, we divide 35 by 10:
$35 \text{ mm} = \frac{35}{10} \text{ cm} = \mathbf{3.5 \text{ cm}}$
To express 35 mm in metres, we divide 35 by 1000:
$35 \text{ mm} = \frac{35}{1000} \text{ m} = \mathbf{0.035 \text{ m}}$
To express 35 mm in kilometres, we divide 35 by 1,000,000:
$35 \text{ mm} = \frac{35}{1000000} \text{ km} = \mathbf{0.000035 \text{ km}}$
Question 4. Express in kg:
(i) 200 g
(ii) 3470 g
(iii) 4 kg 8 g
Answer:
Solution:
We know that $1$ kg $= 1000$ g.
Therefore, $1$ g $= \frac{1}{1000}$ kg $= 0.001$ kg.
To convert grams to kilograms, we divide the number of grams by 1000.
(i) 200 g
$200 \text{ g} = \frac{200}{1000} \text{ kg}$
$= \frac{2}{10} \text{ kg} = \mathbf{0.2 \text{ kg}}$
(ii) 3470 g
$3470 \text{ g} = \frac{3470}{1000} \text{ kg}$
$= \mathbf{3.470 \text{ kg}}$ or $\mathbf{3.47 \text{ kg}}$
(iii) 4 kg 8 g
$4 \text{ kg } 8 \text{ g} = 4 \text{ kg} + 8 \text{ g}$
Convert 8 g to kilograms:
$8 \text{ g} = \frac{8}{1000} \text{ kg} = 0.008 \text{ kg}$
Add this to the existing 4 kg:
Total weight = $4 \text{ kg} + 0.008 \text{ kg} = \mathbf{4.008 \text{ kg}}$
Question 5. Write the following decimal numbers in the expanded form:
(i) 20.03
(ii) 2.03
(iii) 200.03
(iv) 2.034
Answer:
Solution:
The expanded form of a decimal number shows the value of each digit based on its place value.
(i) 20.03
In $20.03$, the digit 2 is in the tens place, 0 is in the ones place, 0 is in the tenths place, and 3 is in the hundredths place.
Expanded form: $2 \times 10 + 0 \times 1 + 0 \times \frac{1}{10} + 3 \times \frac{1}{100}$
This can be written as: $20 + 0 + 0 + \frac{3}{100}$
So, the expanded form of 20.03 is $\mathbf{2 \times 10 + 0 \times 1 + 0 \times \frac{1}{10} + 3 \times \frac{1}{100}}$.
(ii) 2.03
In $2.03$, the digit 2 is in the ones place, 0 is in the tenths place, and 3 is in the hundredths place.
Expanded form: $2 \times 1 + 0 \times \frac{1}{10} + 3 \times \frac{1}{100}$
This can be written as: $2 + 0 + \frac{3}{100}$
So, the expanded form of 2.03 is $\mathbf{2 \times 1 + 0 \times \frac{1}{10} + 3 \times \frac{1}{100}}$.
(iii) 200.03
In $200.03$, the digit 2 is in the hundreds place, 0 is in the tens place, 0 is in the ones place, 0 is in the tenths place, and 3 is in the hundredths place.
Expanded form: $2 \times 100 + 0 \times 10 + 0 \times 1 + 0 \times \frac{1}{10} + 3 \times \frac{1}{100}$
This can be written as: $200 + 0 + 0 + 0 + \frac{3}{100}$
So, the expanded form of 200.03 is $\mathbf{2 \times 100 + 0 \times 10 + 0 \times 1 + 0 \times \frac{1}{10} + 3 \times \frac{1}{100}}$.
(iv) 2.034
In $2.034$, the digit 2 is in the ones place, 0 is in the tenths place, 3 is in the hundredths place, and 4 is in the thousandths place.
Expanded form: $2 \times 1 + 0 \times \frac{1}{10} + 3 \times \frac{1}{100} + 4 \times \frac{1}{1000}$
This can be written as: $2 + 0 + \frac{3}{100} + \frac{4}{1000}$
So, the expanded form of 2.034 is $\mathbf{2 \times 1 + 0 \times \frac{1}{10} + 3 \times \frac{1}{100} + 4 \times \frac{1}{1000}}$.
Question 6. Write the place value of 2 in the following decimal numbers:
(i) 2.56
(ii) 21.37
(iii) 10.25
(iv) 9.42
(v) 63.352
Answer:
Solution:
We need to identify the place value of the digit 2 in each decimal number.
(i) In $2.56$, the digit 2 is in the ones place.
(ii) In $21.37$, the digit 2 is in the tens place.
(iii) In $10.25$, the digit 2 is in the first place after the decimal point, which is the tenths place.
(iv) In $9.42$, the digit 2 is in the second place after the decimal point, which is the hundredths place.
(v) In $63.352$, the digit 2 is in the third place after the decimal point, which is the thousandths place.
Question 7. Dinesh went from place A to place B and from there to place C. A is 7.5 km from B and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A and C is 11.8 km from D. Who travelled more and by how much?
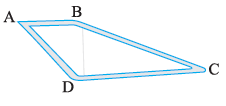
Answer:
To Find:
Who travelled a greater distance, Dinesh or Ayub, and by how much.
Solution:
First, we calculate the total distance travelled by Dinesh and Ayub separately.
Distance travelled by Dinesh:
Dinesh went from place A to B, and then from B to C.
Distance from A to B = 7.5 km
Distance from B to C = 12.7 km
Total distance travelled by Dinesh = Distance (A to B) + Distance (B to C)
$= 7.5 \text{ km} + 12.7 \text{ km}$
$\begin{array}{cc} & 7 & . & 5 \\ + & 12 & . & 7 \\ \hline & 20 & . & 2 \\ \hline \end{array}$
So, Dinesh travelled 20.2 km.
Distance travelled by Ayub:
Ayub went from place A to D, and then from D to C.
Distance from A to D = 9.3 km
Distance from D to C = 11.8 km
Total distance travelled by Ayub = Distance (A to D) + Distance (D to C)
$= 9.3 \text{ km} + 11.8 \text{ km}$
$\begin{array}{cc} & 9 & . & 3 \\ + & 11 & . & 8 \\ \hline & 21 & . & 1 \\ \hline \end{array}$
So, Ayub travelled 21.1 km.
Comparison of Distances:
Now, we compare the total distance travelled by both.
Distance travelled by Dinesh = 20.2 km
Distance travelled by Ayub = 21.1 km
Since $21.1 > 20.2$, Ayub travelled a greater distance.
Ayub travelled more.
By how much?
To find the difference, we subtract the smaller distance from the larger distance.
Difference = Distance travelled by Ayub - Distance travelled by Dinesh
$= 21.1 \text{ km} - 20.2 \text{ km}$
$\begin{array}{cc} & 21 & . & 1 \\ - & 20 & . & 2 \\ \hline & 0 & . & 9 \\ \hline \end{array}$
The difference is 0.9 km.
Therefore, Ayub travelled more than Dinesh by 0.9 km.
Question 8. Shyama bought 5 kg 300 g apples and 3 kg 250 g mangoes. Sarala bought 4 kg 800 g oranges and 4 kg 150 g bananas. Who bought more fruits?
Answer:
Solution:
Given:
Shyama bought: 5 kg 300 g apples and 3 kg 250 g mangoes.
Sarala bought: 4 kg 800 g oranges and 4 kg 150 g bananas.
To Find:
Who bought more fruits.
Solution:
To find who bought more fruits, we need to calculate the total weight of fruits bought by each person and then compare these total weights.
We know that $1$ kg $= 1000$ g.
So, $1$ g $= \frac{1}{1000}$ kg.
Calculate the total weight of fruits bought by Shyama:
Weight of apples = 5 kg 300 g
$= 5 \text{ kg} + 300 \text{ g}$
$= 5 \text{ kg} + \frac{300}{1000} \text{ kg} = 5 \text{ kg} + 0.300 \text{ kg} = 5.300 \text{ kg}$.
Weight of mangoes = 3 kg 250 g
$= 3 \text{ kg} + 250 \text{ g}$
$= 3 \text{ kg} + \frac{250}{1000} \text{ kg} = 3 \text{ kg} + 0.250 \text{ kg} = 3.250 \text{ kg}$.
Total weight bought by Shyama = Weight of apples + Weight of mangoes
$= 5.300 \text{ kg} + 3.250 \text{ kg}$.
Adding the decimal numbers:
$\begin{array}{cc} & 5 & . & 3 & 0 & 0 \\ + & 3 & . & 2 & 5 & 0 \\ \hline & 8 & . & 5 & 5 & 0 \\ \hline \end{array}$
Total weight bought by Shyama = $8.550$ kg or $8.55$ kg.
Calculate the total weight of fruits bought by Sarala:
Weight of oranges = 4 kg 800 g
$= 4 \text{ kg} + 800 \text{ g}$
$= 4 \text{ kg} + \frac{800}{1000} \text{ kg} = 4 \text{ kg} + 0.800 \text{ kg} = 4.800 \text{ kg}$.
Weight of bananas = 4 kg 150 g
$= 4 \text{ kg} + 150 \text{ g}$
$= 4 \text{ kg} + \frac{150}{1000} \text{ kg} = 4 \text{ kg} + 0.150 \text{ kg} = 4.150 \text{ kg}$.
Total weight bought by Sarala = Weight of oranges + Weight of bananas
$= 4.800 \text{ kg} + 4.150 \text{ kg}$.
Adding the decimal numbers:
$\begin{array}{cc} & 4 & . & 8 & 0 & 0 \\ + & 4 & . & 1 & 5 & 0 \\ \hline & 8 & . & 9 & 5 & 0 \\ \hline \end{array}$
Total weight bought by Sarala = $8.950$ kg or $8.95$ kg.
Comparison:
Shyama's total weight = $8.55$ kg.
Sarala's total weight = $8.95$ kg.
Comparing $8.55$ and $8.95$, the whole number parts are the same (8). Comparing the tenths place digits, we have $5$ in $8.55$ and $9$ in $8.95$. Since $9 > 5$, we conclude that $8.95 > 8.55$.
Therefore, Sarala bought more fruits than Shyama.
Sarala bought more fruits.
Question 9. How much less is 28 km than 42.6 km?
Answer:
Solution:
To find out how much less 28 km is than 42.6 km, we need to subtract 28 km from 42.6 km.
This is a subtraction problem: $42.6 - 28$.
We can write 28 as a decimal, $28.0$, to align the decimal points for subtraction.
We need to calculate $42.6 - 28.0$.
Subtracting the numbers:
$\begin{array}{cc} & 4 & 2 & . & 6 \\ - & 2 & 8 & . & 0 \\ \hline & 1 & 4 & . & 6 \\ \hline \end{array}$
The difference is $14.6$.
So, 28 km is 14.6 km less than 42.6 km.
The answer is $\mathbf{14.6}$ km.
Example 7 & 8 (Before Exercise 2.6)
Example 7 The side of an equilateral triangle is 3.5 cm. Find its perimeter.
Answer:
Solution:
Given:
The side length of an equilateral triangle = $3.5$ cm.
To Find:
The perimeter of the equilateral triangle.
Solution:
An equilateral triangle has three sides of equal length.
The perimeter of a triangle is the sum of the lengths of its three sides.
For an equilateral triangle, the perimeter is given by the formula:
Perimeter = $3 \times \text{side length}$
Substitute the given side length into the formula:
Perimeter = $3 \times 3.5$ cm.
Multiply $3$ by $3.5$:
$3 \times 3.5 = 10.5$
So, the perimeter of the equilateral triangle is $10.5$ cm.
Alternatively, we can convert the decimal to a fraction:
$3.5 = 3 \frac{5}{10} = 3 \frac{1}{2} = \frac{(3 \times 2) + 1}{2} = \frac{7}{2}$ cm.
Perimeter = $3 \times \frac{7}{2} = \frac{3 \times 7}{2} = \frac{21}{2}$ cm.
Converting the improper fraction back to a decimal: $\frac{21}{2} = 10.5$ cm.
Thus, the perimeter of the equilateral triangle is $\mathbf{10.5}$ cm.
Example 8 The length of a rectangle is 7.1 cm and its breadth is 2.5 cm. What is the area of the rectangle?
Answer:
Given:
Length of the rectangle = 7.1 cm
Breadth of the rectangle = 2.5 cm
To Find:
The area of the rectangle.
Solution:
The formula for the area of a rectangle is:
Area = Length × Breadth
Substituting the given values into the formula:
Area = $7.1 \text{ cm} \times 2.5 \text{ cm}$
To calculate the product, we first multiply the numbers without the decimal points, i.e., $71 \times 25$.
$\begin{array}{cc} & & 7 & 1 \\ \times & & 2 & 5 \\ \hline & 3 & 5 & 5 \\ 1 & 4 & 2 & \times \\ \hline 1 & 7 & 7 & 5 \\ \hline \end{array}$
Now, we need to place the decimal point in the product. The number of decimal places in 7.1 is one, and the number of decimal places in 2.5 is also one.
Total number of decimal places = 1 + 1 = 2.
So, we place the decimal point two places from the right in the product 1775.
This gives us 17.75.
The area of the rectangle is $17.75$ cm2 (square centimetres).
Therefore, the area of the rectangle is 17.75 cm2.
Exercise 2.6
Question 1. Find:
(i) 0.2 × 6
(ii) 8 × 4.6
(iii) 2.71 × 5
(iv) 20.1 × 4
(v) 0.05 × 7
(vi) 211.02 × 4
(vii) 2 × 0.86
Answer:
Solution:
(i) $0.2 \times 6$
Multiply 2 by 6 ignoring the decimal point: $2 \times 6 = 12$.
The number 0.2 has one decimal place. So, the product will have one decimal place.
Place the decimal point one place from the right in 12: $1.2$.
$0.2 \times 6 = \mathbf{1.2}$.
(ii) $8 \times 4.6$
Multiply 8 by 46 ignoring the decimal point: $8 \times 46 = 368$.
The number 4.6 has one decimal place. So, the product will have one decimal place.
Place the decimal point one place from the right in 368: $36.8$.
$8 \times 4.6 = \mathbf{36.8}$.
(iii) $2.71 \times 5$
Multiply 271 by 5 ignoring the decimal point: $271 \times 5 = 1355$.
The number 2.71 has two decimal places. So, the product will have two decimal places.
Place the decimal point two places from the right in 1355: $13.55$.
$2.71 \times 5 = \mathbf{13.55}$.
(iv) $20.1 \times 4$
Multiply 201 by 4 ignoring the decimal point: $201 \times 4 = 804$.
The number 20.1 has one decimal place. So, the product will have one decimal place.
Place the decimal point one place from the right in 804: $80.4$.
$20.1 \times 4 = \mathbf{80.4}$.
(v) $0.05 \times 7$
Multiply 5 by 7 ignoring the decimal point: $5 \times 7 = 35$.
The number 0.05 has two decimal places. So, the product will have two decimal places.
Place the decimal point two places from the right in 35: $0.35$.
$0.05 \times 7 = \mathbf{0.35}$.
(vi) $211.02 \times 4$
Multiply 21102 by 4 ignoring the decimal point: $21102 \times 4 = 84408$.
The number 211.02 has two decimal places. So, the product will have two decimal places.
Place the decimal point two places from the right in 84408: $844.08$.
$211.02 \times 4 = \mathbf{844.08}$.
(vii) $2 \times 0.86$
Multiply 2 by 86 ignoring the decimal point: $2 \times 86 = 172$.
The number 0.86 has two decimal places. So, the product will have two decimal places.
Place the decimal point two places from the right in 172: $1.72$.
$2 \times 0.86 = \mathbf{1.72}$.
Question 2. Find the area of rectangle whose length is 5.7cm and breadth is 3 cm.
Answer:
Solution:
Given:
Length of the rectangle, $l = 5.7$ cm.
Breadth of the rectangle, $b = 3$ cm.
To Find:
The area of the rectangle.
Solution:
The area of a rectangle is calculated by multiplying its length by its breadth.
$A = \text{length} \times \text{breadth}$
$A = l \times b$
Substitute the given values into the formula:
$A = 5.7 \text{ cm} \times 3 \text{ cm}$
To multiply the decimal number by the whole number, we can multiply them as whole numbers and then place the decimal point in the result.
Multiply 57 by 3:
$\begin{array}{cc}& & 5 & 7 \\ \times & & & 3 \\ \hline & 1 & 7 & 1 \\ \hline \end{array}$
The product of 57 and 3 is 171.
Count the number of decimal places in the original numbers: 5.7 has one decimal place, and 3 has zero decimal places. The total number of decimal places in the product is $1 + 0 = 1$.
Place the decimal point one place from the right in the product 171: $17.1$.
So, the area is $17.1 \text{ cm}^2$.
The area of the rectangle is $\mathbf{17.1 \text{ cm}^2}$.
Question 3. Find:
(i) 1.3 × 10
(ii) 36.8 × 10
(iii) 153.7 × 10
(iv) 168.07 × 10
(v) 31.1 × 100
(vi) 156.1 × 100
(vii) 3.62 × 100
(viii) 43.07 × 100
(ix) 0.5 × 10
(x) 0.08 × 10
(xi) 0.9 × 100
(xii) 0.03 × 1000
Answer:
Solution:
When multiplying a decimal number by 10, 100, or 1000, we shift the decimal point to the right by as many places as there are zeros in 10, 100, or 1000 respectively.
(i) $1.3 \times 10$
Since 10 has one zero, shift the decimal point in 1.3 one place to the right.
$1.3 \times 10 = \mathbf{13}$
(ii) $36.8 \times 10$
Since 10 has one zero, shift the decimal point in 36.8 one place to the right.
$36.8 \times 10 = \mathbf{368}$
(iii) $153.7 \times 10$
Since 10 has one zero, shift the decimal point in 153.7 one place to the right.
$153.7 \times 10 = \mathbf{1537}$
(iv) $168.07 \times 10$
Since 10 has one zero, shift the decimal point in 168.07 one place to the right.
$168.07 \times 10 = \mathbf{1680.7}$
(v) $31.1 \times 100$
Since 100 has two zeros, shift the decimal point in 31.1 two places to the right. We add one zero at the end.
$31.1 \times 100 = 31.10 \times 100 = \mathbf{3110}$
(vi) $156.1 \times 100$
Since 100 has two zeros, shift the decimal point in 156.1 two places to the right. We add one zero at the end.
$156.1 \times 100 = 156.10 \times 100 = \mathbf{15610}$
(vii) $3.62 \times 100$
Since 100 has two zeros, shift the decimal point in 3.62 two places to the right.
$3.62 \times 100 = \mathbf{362}$
(viii) $43.07 \times 100$
Since 100 has two zeros, shift the decimal point in 43.07 two places to the right.
$43.07 \times 100 = \mathbf{4307}$
(ix) $0.5 \times 10$
Since 10 has one zero, shift the decimal point in 0.5 one place to the right.
$0.5 \times 10 = \mathbf{5}$
(x) $0.08 \times 10$
Since 10 has one zero, shift the decimal point in 0.08 one place to the right.
$0.08 \times 10 = \mathbf{0.8}$
(xi) $0.9 \times 100$
Since 100 has two zeros, shift the decimal point in 0.9 two places to the right. We add one zero.
$0.9 \times 100 = 0.90 \times 100 = \mathbf{90}$
(xii) $0.03 \times 1000$
Since 1000 has three zeros, shift the decimal point in 0.03 three places to the right. We add one zero.
$0.03 \times 1000 = 0.030 \times 1000 = \mathbf{30}$
Question 4. A two-wheeler covers a distance of 55.3 km in one litre of petrol. How much distance will it cover in 10 litres of petrol?
Answer:
Solution:
Given:
Distance covered by the two-wheeler in 1 litre of petrol = $55.3$ km.
Quantity of petrol = $10$ litres.
To Find:
The total distance the two-wheeler will cover in 10 litres of petrol.
Solution:
The total distance covered is the product of the distance covered per litre and the total quantity of petrol used.
Total distance = (Distance per litre) $\times$ (Quantity of petrol)
Total distance = $55.3 \text{ km/litre} \times 10 \text{ litres}$.
To multiply a decimal number by 10, we shift the decimal point one place to the right.
$55.3 \times 10 = 553$.
So, the total distance covered is 553 km.
Thus, the two-wheeler will cover a distance of $\mathbf{553}$ km in 10 litres of petrol.
Question 5. Find:
(i) 2.5 × 0.3
(ii) 0.1 × 51.7
(iii) 0.2 × 316.8
(iv) 1.3 × 3.1
(v) 0.5 × 0.05
(vi) 11.2 × 0.15
(vii) 1.07 × 0.02
(viii) 10.05 × 1.05
(ix) 101.01 × 0.01
(x) 100.01 × 1.1
Answer:
Solution:
To multiply decimal numbers, we multiply them as whole numbers and then place the decimal point in the product. The number of decimal places in the product is the sum of the number of decimal places in the numbers being multiplied.
(i) $2.5 \times 0.3$
Multiply 25 by 3: $25 \times 3 = 75$.
2.5 has 1 decimal place. 0.3 has 1 decimal place.
Total decimal places in the product = $1 + 1 = 2$.
Place the decimal point 2 places from the right in 75: $0.75$.
$2.5 \times 0.3 = \mathbf{0.75}$.
(ii) $0.1 \times 51.7$
Multiply 1 by 517: $1 \times 517 = 517$.
0.1 has 1 decimal place. 51.7 has 1 decimal place.
Total decimal places in the product = $1 + 1 = 2$.
Place the decimal point 2 places from the right in 517: $5.17$.
$0.1 \times 51.7 = \mathbf{5.17}$.
(iii) $0.2 \times 316.8$
Multiply 2 by 3168: $2 \times 3168 = 6336$.
0.2 has 1 decimal place. 316.8 has 1 decimal place.
Total decimal places in the product = $1 + 1 = 2$.
Place the decimal point 2 places from the right in 6336: $63.36$.
$0.2 \times 316.8 = \mathbf{63.36}$.
(iv) $1.3 \times 3.1$
Multiply 13 by 31:
$\begin{array}{cc}& & 1 & 3 \\ \times & & 3 & 1 \\ \hline && 1 & 3 \\ & 3 & 9 & \times \\ \hline & 4 & 0 & 3 \\ \hline \end{array}$
The product of 13 and 31 is 403.
1.3 has 1 decimal place. 3.1 has 1 decimal place.
Total decimal places in the product = $1 + 1 = 2$.
Place the decimal point 2 places from the right in 403: $4.03$.
$1.3 \times 3.1 = \mathbf{4.03}$.
(v) $0.5 \times 0.05$
Multiply 5 by 5: $5 \times 5 = 25$.
0.5 has 1 decimal place. 0.05 has 2 decimal places.
Total decimal places in the product = $1 + 2 = 3$.
Place the decimal point 3 places from the right in 25. We add a leading zero: $0.025$.
$0.5 \times 0.05 = \mathbf{0.025}$.
(vi) $11.2 \times 0.15$
Multiply 112 by 15:
$\begin{array}{cc}& & 1 & 1 & 2 \\ \times & & & 1 & 5 \\ \hline && 5 & 6 & 0 \\ & 1 & 1 & 2 & \times \\ \hline & 1 & 6 & 8 & 0 \\ \hline \end{array}$
The product of 112 and 15 is 1680.
11.2 has 1 decimal place. 0.15 has 2 decimal places.
Total decimal places in the product = $1 + 2 = 3$.
Place the decimal point 3 places from the right in 1680: $1.680$, which is $1.68$.
$11.2 \times 0.15 = \mathbf{1.68}$.
(vii) $1.07 \times 0.02$
Multiply 107 by 2: $107 \times 2 = 214$.
1.07 has 2 decimal places. 0.02 has 2 decimal places.
Total decimal places in the product = $2 + 2 = 4$.
Place the decimal point 4 places from the right in 214. We add leading zeros: $0.0214$.
$1.07 \times 0.02 = \mathbf{0.0214}$.
(viii) $10.05 \times 1.05$
Multiply 1005 by 105:
$\begin{array}{cc}& & 1 & 0 & 0 & 5 \\ \times & & & 1 & 0 & 5 \\ \hline && 5 & 0 & 2 & 5 \\ & 0 & 0 & 0 & 0 & \times \\ 1 & 0 & 0 & 5 & \times & \times \\ \hline 1 & 0 & 5 & 5 & 2 & 5 \\ \hline \end{array}$
The product of 1005 and 105 is 105525.
10.05 has 2 decimal places. 1.05 has 2 decimal places.
Total decimal places in the product = $2 + 2 = 4$.
Place the decimal point 4 places from the right in 105525: $10.5525$.
$10.05 \times 1.05 = \mathbf{10.5525}$.
(ix) $101.01 \times 0.01$
Multiply 10101 by 1: $10101 \times 1 = 10101$.
101.01 has 2 decimal places. 0.01 has 2 decimal places.
Total decimal places in the product = $2 + 2 = 4$.
Place the decimal point 4 places from the right in 10101: $1.0101$.
$101.01 \times 0.01 = \mathbf{1.0101}$.
(x) $100.01 \times 1.1$
Multiply 10001 by 11:
$\begin{array}{ccccc}& & 1 & 0 & 0 & 0 & 1 \\ \times & & & & & 1 & 1 \\ \hline && 1 & 0 & 0 & 0 & 1 \\ & 1 & 0 & 0 & 0 & 1 & \times \\ \hline & 1 & 1 & 0 & 0 & 1 & 1 \\ \hline \end{array}$
The product of 10001 and 11 is 110011.
100.01 has 2 decimal places. 1.1 has 1 decimal place.
Total decimal places in the product = $2 + 1 = 3$.
Place the decimal point 3 places from the right in 110011: $110.011$.
$100.01 \times 1.1 = \mathbf{110.011}$.
Example 9 to 11 (Before Exercise 2.7)
Example 9 Find the average of 4.2, 3.8 and 7.6.
Answer:
Solution:
To find the average of a set of numbers, we sum all the numbers and then divide the sum by the total count of numbers.
The given numbers are 4.2, 3.8, and 7.6.
The number of values is 3.
First, calculate the sum of the numbers:
Sum = $4.2 + 3.8 + 7.6$
We add the decimal numbers:
$\begin{array}{cc} & 4 & . & 2 \\ & 3 & . & 8 \\ + & 7 & . & 6 \\ \hline & 1 & 5 & . & 6 \\ \hline \end{array}$
The sum of the numbers is 15.6.
Now, calculate the average:
Average = $\frac{\text{Sum of numbers}}{\text{Number of numbers}}$
Average = $\frac{15.6}{3}$
Divide 15.6 by 3:
$15.6 \div 3 = 5.2$
The average of 4.2, 3.8, and 7.6 is 5.2.
The average is $\mathbf{5.2}$.
Example 10 Each side of a regular polygon is 2.5 cm in length. The perimeter of the polygon is 12.5 cm. How many sides does the polygon have?
Answer:
Solution:
Given:
Length of each side of the regular polygon = $2.5$ cm.
Perimeter of the polygon = $12.5$ cm.
To Find:
The number of sides the polygon has.
Solution:
For a regular polygon, the perimeter is the total length around its boundary. Since all sides of a regular polygon are equal in length, the perimeter is calculated by multiplying the length of one side by the number of sides.
Perimeter = Number of sides $\times$ Length of each side.
Let the number of sides of the polygon be $n$.
We can write the given information as an equation:
$12.5 \text{ cm} = n \times 2.5 \text{ cm}$.
To find the number of sides, $n$, we need to divide the perimeter by the length of each side:
$n = \frac{\text{Perimeter}}{\text{Length of each side}}$
$n = \frac{12.5}{2.5}$
To divide decimal numbers, we can remove the decimal points by multiplying both the numerator and the denominator by the same power of 10. In this case, since both numbers have one decimal place, we multiply by 10:
$n = \frac{12.5 \times 10}{2.5 \times 10} = \frac{125}{25}$
Now, divide 125 by 25:
$125 \div 25 = 5$.
So, the number of sides is 5.
A regular polygon with 5 sides is called a pentagon.
The polygon has 5 sides.
Example 11 A car covers a distance of 89.1 km in 2.2 hours. What is the average distance covered by it in 1 hour?
Answer:
Solution:
Given:
Total distance covered by the car = $89.1$ km.
Total time taken = $2.2$ hours.
To Find:
The average distance covered by the car in 1 hour.
Solution:
The average distance covered by the car in 1 hour is the total distance divided by the total time taken.
Average distance per hour = $\frac{\text{Total distance}}{\text{Total time}}$
Average distance per hour = $\frac{89.1 \text{ km}}{2.2 \text{ hours}}$
To divide $89.1$ by $2.2$, we can multiply both the numerator and the denominator by 10 to remove the decimal point:
$\frac{89.1}{2.2} = \frac{89.1 \times 10}{2.2 \times 10} = \frac{891}{22}$
Now, we divide 891 by 22:
$891 \div 22$
$\begin{array}{r} 40.5 \\ 22{\overline{\smash{\big)}\,891.0}} \\ \underline{-~88\phantom{0.0}} \\ 110\phantom{.0} \\ \underline{-~110\phantom{.0}} \\ 0\phantom{.0} \end{array}$
$891 \div 22 = 40.5$
So, the average distance covered in 1 hour is $40.5$ km.
The average distance covered by the car in 1 hour is $\mathbf{40.5}$ km.
Exercise 2.7
Question 1. Find:
(i) 0.4 ÷ 2
(ii) 0.35 ÷ 5
(iii) 2.48 ÷ 4
(iv) 65.4 ÷ 6
(v) 651.2 ÷ 4
(vi) 14.49 ÷ 7
(vii) 3.96 ÷ 4
(viii) 0.80 ÷ 5
Answer:
Solution:
(i) $0.4 \div 2$
To divide a decimal number by a whole number, we can divide the numbers as if they were whole numbers and then place the decimal point in the quotient such that it has the same number of decimal places as the dividend.
Divide 4 by 2: $4 \div 2 = 2$.
The number 0.4 has one decimal place. So, the quotient will have one decimal place.
Place the decimal point one place from the right in 2: $0.2$.
$0.4 \div 2 = \mathbf{0.2}$.
(ii) $0.35 \div 5$
Divide 35 by 5: $35 \div 5 = 7$.
The number 0.35 has two decimal places. So, the quotient will have two decimal places.
Place the decimal point two places from the right in 7: $0.07$.
$0.35 \div 5 = \mathbf{0.07}$.
(iii) $2.48 \div 4$
Divide 248 by 4: $248 \div 4 = 62$.
The number 2.48 has two decimal places. So, the quotient will have two decimal places.
Place the decimal point two places from the right in 62: $0.62$.
$2.48 \div 4 = \mathbf{0.62}$.
(iv) $65.4 \div 6$
Divide 654 by 6: $654 \div 6 = 109$.
The number 65.4 has one decimal place. So, the quotient will have one decimal place.
Place the decimal point one place from the right in 109: $10.9$.
$65.4 \div 6 = \mathbf{10.9}$.
(v) $651.2 \div 4$
Divide 6512 by 4: $6512 \div 4 = 1628$.
The number 651.2 has one decimal place. So, the quotient will have one decimal place.
Place the decimal point one place from the right in 1628: $162.8$.
$651.2 \div 4 = \mathbf{162.8}$.
(vi) $14.49 \div 7$
Divide 1449 by 7: $1449 \div 7 = 207$.
The number 14.49 has two decimal places. So, the quotient will have two decimal places.
Place the decimal point two places from the right in 207: $2.07$.
$14.49 \div 7 = \mathbf{2.07}$.
(vii) $3.96 \div 4$
Divide 396 by 4: $396 \div 4 = 99$.
The number 3.96 has two decimal places. So, the quotient will have two decimal places.
Place the decimal point two places from the right in 99: $0.99$.
$3.96 \div 4 = \mathbf{0.99}$.
(viii) $0.80 \div 5$
Divide 80 by 5: $80 \div 5 = 16$.
The number 0.80 has two decimal places. So, the quotient will have two decimal places.
Place the decimal point two places from the right in 16: $0.16$.
$0.80 \div 5 = \mathbf{0.16}$.
Question 2. Find:
(i) 4.8 ÷ 10
(ii) 52.5 ÷ 10
(iii) 0.7 ÷ 10
(iv) 33.1 ÷ 10
(v) 272.23 ÷ 10
(vi) 0.56 ÷ 10
(vii) 3.97 ÷10
Answer:
Solution:
When dividing a decimal number by 10, 100, or 1000, we shift the decimal point to the left by as many places as there are zeros in 10, 100, or 1000 respectively.
(i) $4.8 \div 10$
Since 10 has one zero, shift the decimal point in 4.8 one place to the left.
$4.8 \div 10 = \mathbf{0.48}$.
(ii) $52.5 \div 10$
Since 10 has one zero, shift the decimal point in 52.5 one place to the left.
$52.5 \div 10 = \mathbf{5.25}$.
(iii) $0.7 \div 10$
Since 10 has one zero, shift the decimal point in 0.7 one place to the left. Add a leading zero.
$0.7 \div 10 = \mathbf{0.07}$.
(iv) $33.1 \div 10$
Since 10 has one zero, shift the decimal point in 33.1 one place to the left.
$33.1 \div 10 = \mathbf{3.31}$.
(v) $272.23 \div 10$
Since 10 has one zero, shift the decimal point in 272.23 one place to the left.
$272.23 \div 10 = \mathbf{27.223}$.
(vi) $0.56 \div 10$
Since 10 has one zero, shift the decimal point in 0.56 one place to the left. Add a leading zero.
$0.56 \div 10 = \mathbf{0.056}$.
(vii) $3.97 \div 10$
Since 10 has one zero, shift the decimal point in 3.97 one place to the left.
$3.97 \div 10 = \mathbf{0.397}$.
Question 3. Find:
(i) 2.7 ÷ 100
(ii) 0.3 ÷ 100
(iii) 0.78 ÷ 100
(iv) 432.6 ÷ 100
(v) 23.6 ÷100
(vi) 98.53 ÷ 100
Answer:
Solution:
When dividing a decimal number by 100, we shift the decimal point to the left by two places.
(i) $2.7 \div 100$
Shift the decimal point in 2.7 two places to the left. We need to add a leading zero.
$2.7 \div 100 = \mathbf{0.027}$.
(ii) $0.3 \div 100$
Shift the decimal point in 0.3 two places to the left. We need to add two leading zeros (one before the original decimal point and one after).
$0.3 \div 100 = \mathbf{0.003}$.
(iii) $0.78 \div 100$
Shift the decimal point in 0.78 two places to the left. We need to add a leading zero.
$0.78 \div 100 = \mathbf{0.0078}$.
(iv) $432.6 \div 100$
Shift the decimal point in 432.6 two places to the left.
$432.6 \div 100 = \mathbf{4.326}$.
(v) $23.6 \div 100$
Shift the decimal point in 23.6 two places to the left.
$23.6 \div 100 = \mathbf{0.236}$.
(vi) $98.53 \div 100$
Shift the decimal point in 98.53 two places to the left.
$98.53 \div 100 = \mathbf{0.9853}$.
Question 4. Find:
(i) 7.9 ÷ 1000
(ii) 26.3 ÷ 1000
(iii) 38.53 ÷ 1000
(iv) 128.9 ÷ 1000
(v) 0.5 ÷ 1000
Answer:
Solution:
When dividing a decimal number by 1000, we shift the decimal point to the left by three places.
(i) $7.9 \div 1000$
Shift the decimal point in 7.9 three places to the left. We need to add two leading zeros.
$7.9 \div 1000 = \mathbf{0.0079}$.
(ii) $26.3 \div 1000$
Shift the decimal point in 26.3 three places to the left. We need to add one leading zero.
$26.3 \div 1000 = \mathbf{0.0263}$.
(iii) $38.53 \div 1000$
Shift the decimal point in 38.53 three places to the left. We need to add one leading zero.
$38.53 \div 1000 = \mathbf{0.03853}$.
(iv) $128.9 \div 1000$
Shift the decimal point in 128.9 three places to the left.
$128.9 \div 1000 = \mathbf{0.1289}$.
(v) $0.5 \div 1000$
Shift the decimal point in 0.5 three places to the left. We need to add three leading zeros (one for the original zero and two more).
$0.5 \div 1000 = \mathbf{0.0005}$.
Question 5. Find:
(i) 7 ÷ 3.5
(ii) 36 ÷ 0.2
(iii) 3.25 ÷ 0.5
(iv) 30.94 ÷ 0.7
(v) 0.5 ÷ 0.25
(vi) 7.75 ÷ 0.25
(vii) 76.5 ÷ 0.15
(viii) 37.8 ÷ 1.4
(ix) 2.73 ÷ 1.3
Answer:
Solution:
To divide a decimal number by another decimal number, we convert the divisor into a whole number by shifting the decimal point in both the dividend and the divisor by the same number of places to the right.
(i) $7 \div 3.5$
Shift the decimal point 1 place to the right in 3.5 to make it 35. Shift the decimal point 1 place to the right in 7 (or 7.0) to make it 70.
So, $7 \div 3.5 = 70 \div 35$.
$70 \div 35 = 2$.
The answer is $\mathbf{2}$.
(ii) $36 \div 0.2$
Shift the decimal point 1 place to the right in 0.2 to make it 2. Shift the decimal point 1 place to the right in 36 (or 36.0) to make it 360.
So, $36 \div 0.2 = 360 \div 2$.
$360 \div 2 = 180$.
The answer is $\mathbf{180}$.
(iii) $3.25 \div 0.5$
Shift the decimal point 1 place to the right in 0.5 to make it 5. Shift the decimal point 1 place to the right in 3.25 to make it 32.5.
So, $3.25 \div 0.5 = 32.5 \div 5$.
Divide 32.5 by 5:
$\begin{array}{r} 6.5 \\ 5{\overline{\smash{\big)}\,32.5}} \\ \underline{-~30\phantom{.0}} \\ 25\phantom{0} \\ \underline{-~25\phantom{0}} \\ 0\phantom{0} \end{array}$
$32.5 \div 5 = 6.5$.
The answer is $\mathbf{6.5}$.
(iv) $30.94 \div 0.7$
Shift the decimal point 1 place to the right in 0.7 to make it 7. Shift the decimal point 1 place to the right in 30.94 to make it 309.4.
So, $30.94 \div 0.7 = 309.4 \div 7$.
Divide 309.4 by 7:
$\begin{array}{r} 44.2 \\ 7{\overline{\smash{\big)}\,309.4}} \\ \underline{-~28\phantom{0.0}} \\ 29\phantom{.0} \\ \underline{-~28\phantom{.0}} \\ 14\phantom{0} \\ \underline{-~14\phantom{0}} \\ 0\phantom{0} \end{array}$
$309.4 \div 7 = 44.2$.
The answer is $\mathbf{44.2}$.
(v) $0.5 \div 0.25$
Shift the decimal point 2 places to the right in 0.25 to make it 25. Shift the decimal point 2 places to the right in 0.5 (or 0.50) to make it 50.
So, $0.5 \div 0.25 = 50 \div 25$.
$50 \div 25 = 2$.
The answer is $\mathbf{2}$.
(vi) $7.75 \div 0.25$
Shift the decimal point 2 places to the right in 0.25 to make it 25. Shift the decimal point 2 places to the right in 7.75 to make it 775.
So, $7.75 \div 0.25 = 775 \div 25$.
Divide 775 by 25:
$\begin{array}{r} 31 \\ 25{\overline{\smash{\big)}\,775}} \\ \underline{-~75\phantom{0}} \\ 25 \\ \underline{-~25} \\ 0 \end{array}$
$775 \div 25 = 31$.
The answer is $\mathbf{31}$.
(vii) $76.5 \div 0.15$
Shift the decimal point 2 places to the right in 0.15 to make it 15. Shift the decimal point 2 places to the right in 76.5 (or 76.50) to make it 7650.
So, $76.5 \div 0.15 = 7650 \div 15$.
Divide 7650 by 15:
$\begin{array}{r} 510 \\ 15{\overline{\smash{\big)}\,7650}} \\ \underline{-~75\phantom{00}} \\ 15\phantom{0} \\ \underline{-~15\phantom{0}} \\ 00 \end{array}$
$7650 \div 15 = 510$.
The answer is $\mathbf{510}$.
(viii) $37.8 \div 1.4$
Shift the decimal point 1 place to the right in 1.4 to make it 14. Shift the decimal point 1 place to the right in 37.8 to make it 378.
So, $37.8 \div 1.4 = 378 \div 14$.
Divide 378 by 14:
$\begin{array}{r} 27 \\ 14{\overline{\smash{\big)}\,378}} \\ \underline{-~28\phantom{0}} \\ 98 \\ \underline{-~98} \\ 0 \end{array}$
$378 \div 14 = 27$.
The answer is $\mathbf{27}$.
(ix) $2.73 \div 1.3$
Shift the decimal point 1 place to the right in 1.3 to make it 13. Shift the decimal point 1 place to the right in 2.73 to make it 27.3.
So, $2.73 \div 1.3 = 27.3 \div 13$.
Divide 27.3 by 13:
$\begin{array}{r} 2.1 \\ 13{\overline{\smash{\big)}\,27.3}} \\ \underline{-~26\phantom{.0}} \\ 13\phantom{0} \\ \underline{-~13\phantom{0}} \\ 0\phantom{0} \end{array}$
$27.3 \div 13 = 2.1$.
The answer is $\mathbf{2.1}$.
Question 6. A vehicle covers a distance of 43.2 km in 2.4 litres of petrol. How much distance will it cover in one litre of petrol?
Answer:
Solution:
Given:
Total distance covered by the vehicle = $43.2$ km.
Quantity of petrol consumed = $2.4$ litres.
To Find:
Distance covered by the vehicle in one litre of petrol.
Solution:
The distance covered by the vehicle in one litre of petrol is obtained by dividing the total distance covered by the total quantity of petrol consumed.
Distance covered per litre = $\frac{\text{Total distance covered}}{\text{Total quantity of petrol consumed}}$
Distance covered per litre = $\frac{43.2 \text{ km}}{2.4 \text{ litres}}$
To perform the division of decimal numbers, we can multiply both the numerator and the denominator by the same power of 10 to remove the decimal points. Since both 43.2 and 2.4 have one decimal place, we multiply by 10.
$\frac{43.2}{2.4} = \frac{43.2 \times 10}{2.4 \times 10} = \frac{432}{24}$
Now, we need to divide 432 by 24.
$\begin{array}{r} 18 \\ 24{\overline{\smash{\big)}\,432}} \\ \underline{-~24\phantom{0}} \\ 192 \\ \underline{-~192} \\ 0 \end{array}$
The result of the division is 18.
So, the distance covered by the vehicle in one litre of petrol is 18 km.
Thus, the vehicle will cover $\mathbf{18}$ km in one litre of petrol.

